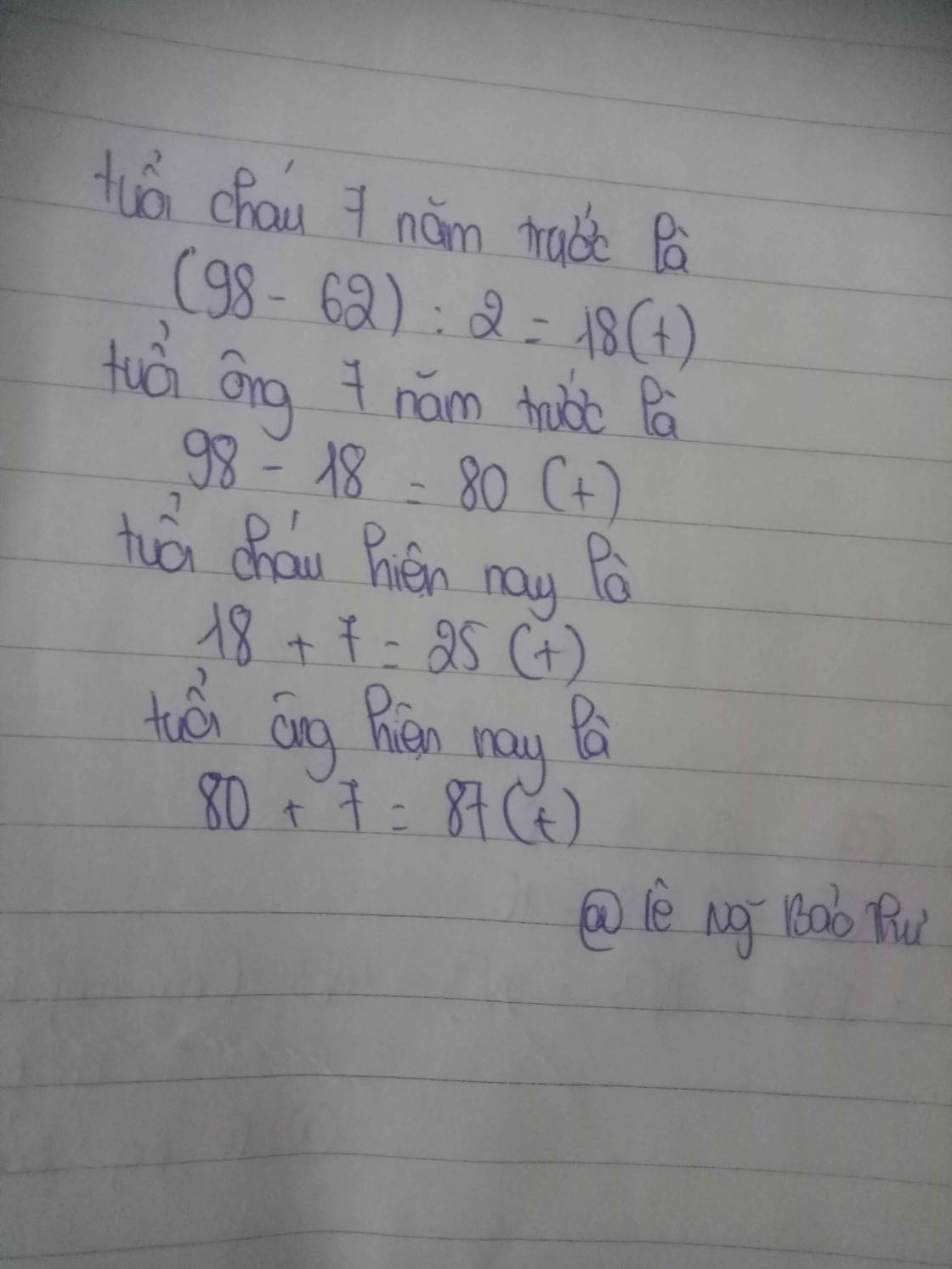Ông Hơn Cháu 56 Tuổi Biết Rằng 3 Năm Nữa: Giải Bài Toán Tuổi Đầy Thú Vị

Bài toán về tuổi tác giữa ông và cháu là một dạng toán phổ biến trong chương trình tiểu học, giúp rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề. Trong bài toán này, ta biết rằng ông hơn cháu 56 tuổi, và sau 3 năm nữa, tổng số tuổi của hai ông cháu sẽ là 80 tuổi. Yêu cầu đặt ra là xác định tuổi hiện tại của ông và cháu.

Để giải quyết bài toán này, ta cần sử dụng phương pháp tìm hai số khi biết tổng và hiệu của chúng. Đây là một phương pháp quan trọng trong toán học, giúp học sinh phát triển khả năng phân tích và giải quyết các bài toán thực tế liên quan đến quan hệ giữa các số.

Để giải bài toán này, ta cần xác định tuổi hiện tại của ông và cháu dựa trên các thông tin sau:

• Hiệu số tuổi giữa ông và cháu: 56 tuổi.
• Sau 3 năm nữa, tổng số tuổi của hai ông cháu: 80 tuổi.

Giả sử tuổi hiện tại của ông là \( x \) và tuổi hiện tại của cháu là \( y \). Theo đề bài, ta có hai phương trình:

• \( x - y = 56 \) (1)
• \( (x + 3) + (y + 3) = 80 \) (2)

Phương trình (2) có thể được đơn giản hóa thành:

• \( x + y + 6 = 80 \)
• \( x + y = 74 \) (3)

Như vậy, ta có hệ phương trình:

• \( x - y = 56 \) (1)
• \( x + y = 74 \) (3)

Giải hệ phương trình này sẽ giúp chúng ta tìm được tuổi hiện tại của ông và cháu.

Để giải bài toán này, ta sử dụng phương pháp giải hệ phương trình dựa trên tổng và hiệu của hai số. Giả sử tuổi hiện tại của ông là \( x \) và tuổi hiện tại của cháu là \( y \). Theo đề bài, ta có hai phương trình:

• \( x - y = 56 \) (hiệu số tuổi giữa ông và cháu)
• \( (x + 3) + (y + 3) = 80 \) (tổng số tuổi của ông và cháu sau 3 năm nữa)

Phương trình thứ hai có thể được viết lại thành:

• \( x + y + 6 = 80 \)
• \( x + y = 74 \) (tổng số tuổi hiện tại của ông và cháu)

Như vậy, ta có hệ phương trình:

• \( x - y = 56 \)
• \( x + y = 74 \)

Giải hệ phương trình này bằng cách cộng hai phương trình lại:

• \( (x - y) + (x + y) = 56 + 74 \)
• \( 2x = 130 \)
• \( x = 65 \)

Thay giá trị của \( x \) vào phương trình \( x + y = 74 \):

• \( 65 + y = 74 \)
• \( y = 9 \)

Vậy, tuổi hiện tại của ông là 65 tuổi và tuổi hiện tại của cháu là 9 tuổi.

Để giải bài toán này, ta thực hiện các bước sau:

1. Xác định tổng số tuổi của hai ông cháu hiện nay:

   Biết rằng sau 3 năm nữa, tổng số tuổi của hai ông cháu là 80 tuổi. Do đó, tổng số tuổi hiện nay của họ là:

   \[ 80 - 3 \times 2 = 80 - 6 = 74 \text{ tuổi} \]

2. Xác định tuổi hiện tại của ông và cháu:

   Giả sử tuổi hiện nay của ông là \( x \) và của cháu là \( y \). Theo đề bài, ta có hai phương trình:

   \[ x - y = 56 \quad \text{(1)} \] \[ x + y = 74 \quad \text{(2)} \]

   Giải hệ phương trình này bằng cách cộng (1) và (2):

   \[ (x - y) + (x + y) = 56 + 74 \] \[ 2x = 130 \implies x = \frac{130}{2} = 65 \text{ tuổi} \]

   Thay \( x = 65 \) vào phương trình (2):

   \[ 65 + y = 74 \implies y = 74 - 65 = 9 \text{ tuổi} \]

Vậy, hiện nay ông 65 tuổi và cháu 9 tuổi.

Để đảm bảo tính chính xác của kết quả, chúng ta kiểm tra lại các điều kiện đã cho trong bài toán:

1. Hiệu số tuổi giữa ông và cháu:

   Tuổi hiện tại của ông là 65 tuổi và của cháu là 9 tuổi. Hiệu số tuổi giữa hai người là:

   \[ 65 - 9 = 56 \text{ tuổi} \]

   Kết quả này phù hợp với điều kiện ông hơn cháu 56 tuổi.

2. Tổng số tuổi của ông và cháu sau 3 năm nữa:

   Sau 3 năm, tuổi của ông sẽ là:

   \[ 65 + 3 = 68 \text{ tuổi} \]

   Tuổi của cháu sẽ là:

   \[ 9 + 3 = 12 \text{ tuổi} \]

   Tổng số tuổi của hai ông cháu sau 3 năm nữa là:

   \[ 68 + 12 = 80 \text{ tuổi} \]

   Kết quả này phù hợp với điều kiện tổng số tuổi của hai ông cháu sẽ là 80 tuổi sau 3 năm nữa.

Như vậy, các kết quả tính toán đều thỏa mãn các điều kiện đã cho trong bài toán, xác nhận rằng tuổi hiện tại của ông là 65 tuổi và của cháu là 9 tuổi.

Để mở rộng bài toán "Ông hơn cháu 56 tuổi, biết rằng 3 năm nữa tổng số tuổi của ông và cháu là 80 tuổi", chúng ta có thể thay đổi các giá trị trong bài toán để tạo ra những tình huống mới và thách thức hơn. Dưới đây là một số ví dụ:

• Ví dụ 1:

  Giả sử ông hơn cháu 50 tuổi, và sau 5 năm nữa, tổng số tuổi của ông và cháu là 90 tuổi. Hỏi hiện nay ông và cháu bao nhiêu tuổi?

  Giải:

  Gọi tuổi hiện tại của ông là \( x \) và của cháu là \( y \). Ta có hệ phương trình:

  • \( x - y = 50 \)
  • \( (x + 5) + (y + 5) = 90 \)

  Giải hệ phương trình này, ta tìm được \( x = 65 \) và \( y = 15 \). Vậy, hiện nay ông 65 tuổi và cháu 15 tuổi.

• Ví dụ 2:

  Giả sử ông hơn cháu 60 tuổi, và sau 2 năm nữa, tổng số tuổi của ông và cháu là 70 tuổi. Hỏi hiện nay ông và cháu bao nhiêu tuổi?

  Giải:

  Gọi tuổi hiện tại của ông là \( x \) và của cháu là \( y \). Ta có hệ phương trình:

  • \( x - y = 60 \)
  • \( (x + 2) + (y + 2) = 70 \)

  Giải hệ phương trình này, ta tìm được \( x = 65 \) và \( y = 5 \). Vậy, hiện nay ông 65 tuổi và cháu 5 tuổi.

• Ví dụ 3:

  Giả sử ông hơn cháu 55 tuổi, và sau 4 năm nữa, tổng số tuổi của ông và cháu là 85 tuổi. Hỏi hiện nay ông và cháu bao nhiêu tuổi?

  Giải:

  Gọi tuổi hiện tại của ông là \( x \) và của cháu là \( y \). Ta có hệ phương trình:

  • \( x - y = 55 \)
  • \( (x + 4) + (y + 4) = 85 \)

  Giải hệ phương trình này, ta tìm được \( x = 65 \) và \( y = 10 \). Vậy, hiện nay ông 65 tuổi và cháu 10 tuổi.

Những ví dụ trên giúp chúng ta hiểu rõ hơn về cách giải bài toán liên quan đến tổng và hiệu tuổi, đồng thời mở rộng khả năng tư duy và ứng dụng trong các tình huống thực tế.

Qua việc giải bài toán "Ông hơn cháu 56 tuổi, biết rằng 3 năm nữa tổng số tuổi của ông và cháu là 80 tuổi", chúng ta đã xác định được:

• Tuổi hiện tại của ông: 65 tuổi
• Tuổi hiện tại của cháu: 9 tuổi

Phương pháp giải sử dụng hệ phương trình dựa trên các mối quan hệ giữa tổng và hiệu tuổi, giúp chúng ta tìm ra lời giải chính xác. Bài toán không chỉ rèn luyện kỹ năng giải toán mà còn khuyến khích tư duy logic và khả năng phân tích vấn đề. Việc mở rộng bài toán với các điều kiện khác nhau cũng tạo cơ hội để áp dụng kiến thức vào nhiều tình huống thực tiễn, nâng cao khả năng tư duy và sáng tạo của người học.