Chủ đề phương pháp giải bài toán tính tuổi lớp 3: Bài viết này sẽ giúp các bậc phụ huynh và học sinh lớp 3 nắm vững phương pháp giải bài toán tính tuổi một cách đơn giản và dễ hiểu. Với những phương pháp rõ ràng, minh bạch, bài viết cung cấp công thức, ví dụ cụ thể và những mẹo nhỏ để học sinh có thể áp dụng hiệu quả trong các bài kiểm tra và bài tập tại lớp.
Mục lục
1. Giới thiệu chung về các bài toán tính tuổi
Bài toán tính tuổi là một dạng toán phổ biến trong chương trình toán học lớp 3, giúp học sinh rèn luyện khả năng suy luận và áp dụng các phép tính cơ bản như cộng, trừ. Mục tiêu của bài toán là tính toán sự chênh lệch giữa hai mốc thời gian, thường là giữa tuổi của các nhân vật hoặc giữa các sự kiện trong quá khứ và hiện tại.
Để giải quyết các bài toán này, học sinh cần hiểu rõ về cách tính số năm, số tháng hoặc số ngày giữa hai thời điểm. Thông qua đó, các em cũng sẽ học cách chuyển đổi giữa các đơn vị thời gian khác nhau, từ đó làm quen với những bài toán phức tạp hơn trong tương lai.
- Ví dụ đơn giản: Nếu tuổi của một người hiện tại là 10 và năm sau sẽ là bao nhiêu?
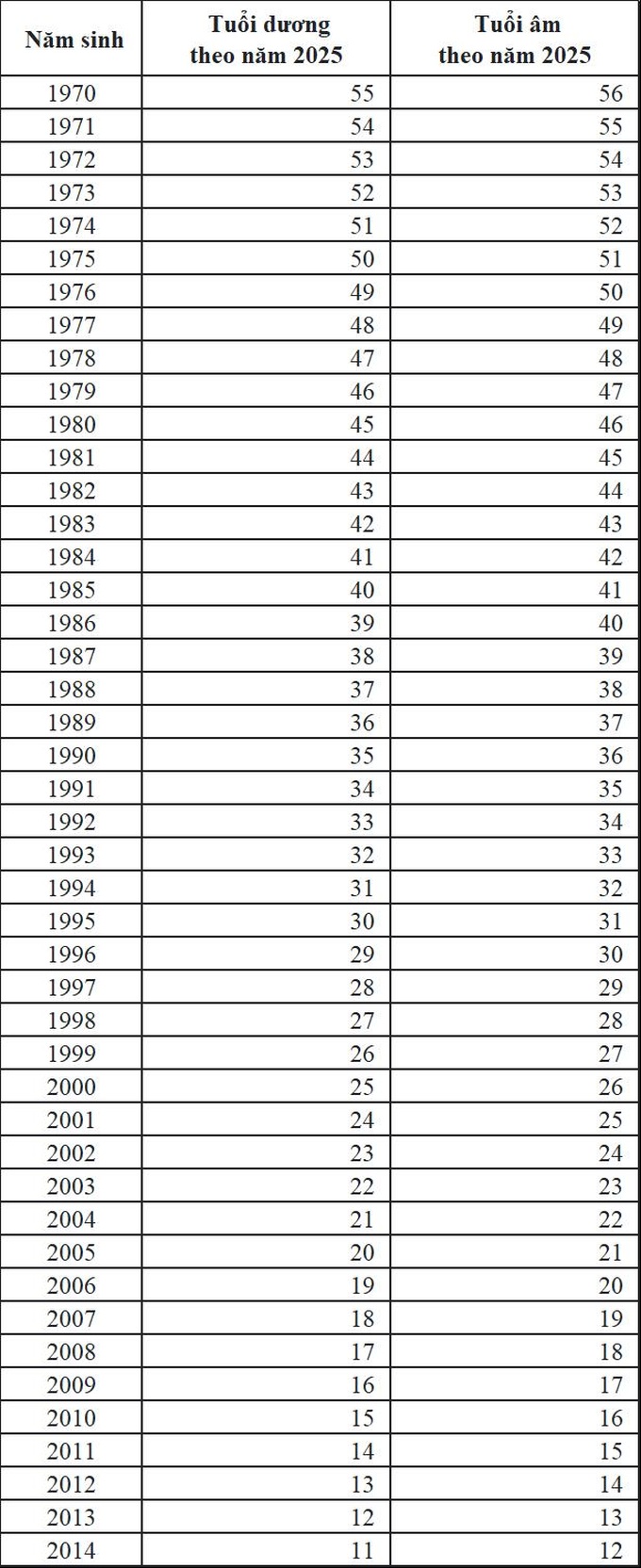
- Ví dụ phức tạp: Nếu năm nay là 2025, và một người sinh năm 2005, hãy tính tuổi của người đó trong năm nay.
Đây là những dạng bài tập thường gặp và sẽ được áp dụng vào các bài toán thực tế trong cuộc sống hàng ngày. Việc giải các bài toán tính tuổi sẽ giúp học sinh nâng cao khả năng tư duy logic, đồng thời hiểu rõ hơn về các đơn vị thời gian.
.png)
2. Các dạng bài toán tính tuổi phổ biến
Các bài toán tính tuổi lớp 3 thường được chia thành một số dạng cơ bản, giúp học sinh làm quen và luyện tập các kỹ năng tính toán đơn giản. Dưới đây là một số dạng bài toán tính tuổi phổ biến mà học sinh sẽ gặp phải:
- Dạng 1: Tính tuổi của một người vào một thời điểm trong tương lai hoặc quá khứ
Đây là dạng bài toán cơ bản, trong đó học sinh sẽ tính tuổi của một người vào một năm cụ thể trong tương lai hoặc quá khứ, dựa trên năm sinh đã cho. Ví dụ: "Nếu bạn sinh năm 2010, thì năm 2025 bạn sẽ bao nhiêu tuổi?"
- Dạng 2: Tính khoảng cách tuổi giữa hai người
Trong bài toán này, học sinh sẽ tính sự chênh lệch tuổi giữa hai người, thông qua năm sinh của mỗi người. Ví dụ: "Anh Nam sinh năm 2000, còn em Linh sinh năm 2005. Hỏi Nam hơn Linh bao nhiêu tuổi?"
- Dạng 3: Tính tuổi hiện tại khi biết năm sinh và năm hiện tại
Đây là dạng bài toán yêu cầu học sinh tính tuổi của một người trong năm hiện tại, biết năm sinh của người đó. Ví dụ: "Cô Mai sinh năm 1990, vậy năm nay cô Mai bao nhiêu tuổi?"
- Dạng 4: Tính năm sinh khi biết tuổi và năm hiện tại
Ở dạng bài này, học sinh sẽ tính được năm sinh của một người khi biết tuổi của họ và năm hiện tại. Ví dụ: "Bạn Lan năm nay 12 tuổi, vậy bạn Lan sinh năm nào?"
Các dạng bài toán này đều giúp học sinh phát triển khả năng tính toán và nâng cao sự hiểu biết về các mốc thời gian. Qua việc giải các bài toán tính tuổi, học sinh cũng sẽ rèn luyện khả năng làm việc với các phép toán cơ bản, đồng thời chuẩn bị cho các bài toán phức tạp hơn trong các lớp học sau này.
3. Các phương pháp giải bài toán tính tuổi
Để giải bài toán tính tuổi một cách hiệu quả, học sinh lớp 3 cần áp dụng các phương pháp đơn giản, dễ hiểu nhưng vô cùng hữu ích. Dưới đây là một số phương pháp phổ biến giúp giải quyết các bài toán tính tuổi:
- Phương pháp 1: Cộng hoặc trừ năm, tháng, ngày
Đây là phương pháp cơ bản và dễ dàng nhất để giải các bài toán tính tuổi. Nếu bài toán yêu cầu tính tuổi trong một năm cụ thể, học sinh chỉ cần cộng hoặc trừ số năm từ năm sinh đến năm cần tính. Ví dụ: "Nếu bạn sinh năm 2010, năm 2025 bạn sẽ bao nhiêu tuổi?" Để giải, ta lấy 2025 trừ đi 2010, kết quả là 15 tuổi.
- Phương pháp 2: Tính chênh lệch giữa hai mốc thời gian
Phương pháp này được áp dụng khi bài toán yêu cầu tìm sự chênh lệch tuổi giữa hai người hoặc hai sự kiện. Để giải bài toán này, học sinh cần tính năm sinh của cả hai người và sau đó lấy năm lớn trừ đi năm nhỏ để tìm ra sự chênh lệch. Ví dụ: "Anh Nam sinh năm 2000, còn em Linh sinh năm 2005. Hỏi Nam hơn Linh bao nhiêu tuổi?" Ta lấy 2005 trừ đi 2000, kết quả là 5 năm.
- Phương pháp 3: Áp dụng công thức tính tuổi
Để tính tuổi chính xác hơn, học sinh có thể sử dụng công thức sau: \[ \text{Tuổi hiện tại} = \text{Năm hiện tại} - \text{Năm sinh} \] Ví dụ: Nếu bạn sinh năm 2010, và năm nay là 2025, ta áp dụng công thức: 2025 - 2010 = 15 tuổi.
- Phương pháp 4: Tính tuổi theo tháng và ngày
Đối với những bài toán yêu cầu tính tuổi theo tháng hoặc ngày, học sinh sẽ cần chuyển đổi giữa các đơn vị thời gian. Ví dụ: "Bạn sinh ngày 15 tháng 3 năm 2010, hôm nay là ngày 15 tháng 3 năm 2025, bạn bao nhiêu tuổi?" Phương pháp này yêu cầu học sinh xác định đúng số tháng hoặc số ngày và sau đó tính tổng tuổi theo đơn vị tháng hoặc năm.
Áp dụng các phương pháp này sẽ giúp học sinh không chỉ giải quyết bài toán tính tuổi mà còn rèn luyện khả năng làm việc với các phép toán cơ bản và cải thiện khả năng tư duy logic. Mỗi phương pháp đều có thể được sử dụng linh hoạt tùy vào dạng bài toán cụ thể.

4. Ví dụ về bài toán nâng cao
Bài toán nâng cao giúp học sinh phát triển tư duy và khả năng giải quyết các tình huống phức tạp hơn trong cuộc sống. Dưới đây là một ví dụ về bài toán tính tuổi nâng cao dành cho học sinh lớp 3:
Ví dụ 1:
"Anh Tuấn sinh năm 2005, còn em Bình sinh năm 2010. Hỏi năm 2025, tuổi của anh Tuấn sẽ gấp bao nhiêu lần tuổi của em Bình?"
Giải:
- Đầu tiên, ta tính tuổi của anh Tuấn và em Bình trong năm 2025.
- Tuổi của anh Tuấn: 2025 - 2005 = 20 tuổi.
- Tuổi của em Bình: 2025 - 2010 = 15 tuổi.
- Sau đó, ta tính tỷ lệ giữa tuổi của anh Tuấn và em Bình trong năm 2025:
- Tỷ lệ tuổi: 20 / 15 = 4/3.
- Vậy, năm 2025, tuổi của anh Tuấn sẽ gấp 4/3 lần tuổi của em Bình.
Ví dụ 2:
"Trong một gia đình, mẹ sinh năm 1980 và con sinh năm 2010. Hỏi sau bao nhiêu năm nữa, tuổi của mẹ sẽ gấp đôi tuổi của con?"
Giải: - Gọi x là số năm sau mà tuổi của mẹ sẽ gấp đôi tuổi của con. Ta có phương trình: \[ (1980 + x) - 1980 = 2 \times ((2010 + x) - 2010) \] - Giải phương trình, ta tìm được x = 10. - Vậy, sau 10 năm, tuổi của mẹ sẽ gấp đôi tuổi của con.
Các bài toán nâng cao không chỉ giúp học sinh áp dụng những kiến thức cơ bản mà còn khuyến khích các em phát triển khả năng tư duy và giải quyết vấn đề. Việc giải quyết các bài toán phức tạp sẽ giúp học sinh tự tin hơn trong việc xử lý các tình huống toán học trong tương lai.
5. Kết luận
Phương pháp giải bài toán tính tuổi lớp 3 không chỉ giúp học sinh làm quen với các phép toán cơ bản mà còn giúp các em rèn luyện khả năng tư duy logic, tính toán nhanh và chính xác. Việc giải quyết các bài toán này giúp học sinh hiểu rõ hơn về các đơn vị thời gian, đồng thời áp dụng được những kiến thức toán học vào thực tế.
Thông qua việc học các dạng bài toán tính tuổi, học sinh không chỉ phát triển kỹ năng tính toán mà còn học được cách giải quyết vấn đề một cách khoa học và có hệ thống. Đây là nền tảng quan trọng để các em tiếp tục chinh phục các bài toán phức tạp hơn trong tương lai.
Hy vọng rằng các phương pháp và ví dụ đã được trình bày sẽ giúp các em học sinh lớp 3 cảm thấy tự tin và hứng thú hơn khi học toán, đồng thời giúp các bậc phụ huynh có thể hỗ trợ con em mình một cách hiệu quả nhất trong quá trình học tập.