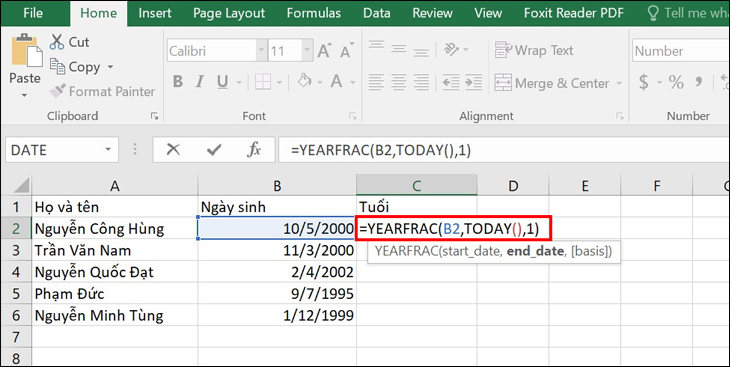
Chủ đề toán tính tuổi lớp 5: Toán Tính Tuổi Lớp 5 là một chủ đề thú vị và bổ ích giúp học sinh rèn luyện kỹ năng tính toán, tư duy logic. Trong bài viết này, bạn sẽ tìm thấy các bài tập, phương pháp giải quyết, và những ví dụ cụ thể giúp các em học sinh nắm vững kiến thức và tự tin giải quyết các bài toán liên quan đến tính tuổi.
Mục lục
- Dạng Bài Toán Cơ Bản: Tính Tuổi Khi Biết Tỉ Số Tuổi
- Dạng Bài Toán Tính Tuổi Khi Biết Tổng Và Tỉ Số Tuổi
- Dạng Bài Toán Tính Tuổi Với Sự Thay Đổi Tỉ Số Tuổi Theo Thời Gian
- Dạng Bài Toán Với Số Thập Phân
- Dạng Bài Toán Khó Hơn: Giải Bài Toán Phức Tạp Về Tuổi Của Các Thành Viên Gia Đình
- Phương Pháp Và Kỹ Thuật Giải Toán Tính Tuổi Lớp 5
Dạng Bài Toán Cơ Bản: Tính Tuổi Khi Biết Tỉ Số Tuổi
Trong bài toán tính tuổi khi biết tỉ số tuổi, bạn sẽ gặp phải những tình huống liên quan đến mối quan hệ giữa tuổi của hai hoặc nhiều người. Thường thì bài toán này yêu cầu bạn tính tuổi của từng người khi biết tỉ số giữa các độ tuổi của họ tại một thời điểm nhất định.
Ví dụ: Nếu tỉ số tuổi của hai người A và B là 3:4, và sau 5 năm nữa, tuổi của A sẽ gấp đôi tuổi của B. Cách giải là bạn sẽ thiết lập phương trình dựa trên mối quan hệ tỉ lệ và sau đó giải để tìm ra độ tuổi cụ thể của từng người.
Dưới đây là các bước cơ bản để giải bài toán dạng này:
- Xác định tỉ số tuổi giữa các đối tượng trong bài toán.
- Đặt ẩn số đại diện cho độ tuổi của các đối tượng.
- Thiết lập phương trình dựa trên mối quan hệ tỉ lệ hoặc các yếu tố liên quan đến thời gian.
- Giải phương trình để tìm giá trị của ẩn số, từ đó tính được độ tuổi cụ thể của các đối tượng.
Ví dụ chi tiết:
| Bài toán | Tìm độ tuổi của A và B khi biết tỉ số tuổi là 3:4 và sau 5 năm nữa, tuổi A sẽ gấp đôi tuổi B. |
| Cách giải |
|
Qua ví dụ này, bạn có thể thấy rõ cách thức giải bài toán tính tuổi khi biết tỉ số tuổi. Thực hành thường xuyên sẽ giúp bạn nắm vững phương pháp và tự tin giải quyết các bài toán tương tự.
.png)
Dạng Bài Toán Tính Tuổi Khi Biết Tổng Và Tỉ Số Tuổi
Dạng bài toán này yêu cầu bạn tính tuổi của hai hoặc nhiều người khi biết tổng tuổi của họ và tỉ số giữa các độ tuổi. Đây là dạng bài toán khá thú vị và thường xuất hiện trong các bài kiểm tra Toán lớp 5, giúp học sinh rèn luyện khả năng suy luận và giải quyết vấn đề.
Để giải bài toán này, bạn cần thực hiện các bước sau:
- Gọi tuổi của các đối tượng là các ẩn số. Ví dụ, nếu có hai người A và B, bạn có thể gọi tuổi của A là \(x\) và tuổi của B là \(y\).
- Viết phương trình dựa trên tỉ số tuổi. Ví dụ, nếu tỉ số tuổi của A và B là 3:5, bạn sẽ có mối quan hệ \(x : y = 3 : 5\), tức là \(y = \frac{5}{3}x\).
- Viết phương trình tổng tuổi. Nếu tổng tuổi của A và B là 36, bạn sẽ có phương trình \(x + y = 36\).
- Sử dụng phương trình tỉ số và phương trình tổng tuổi để giải tìm ra các giá trị của \(x\) và \(y\).
Ví dụ chi tiết:
| Bài toán | Tuổi của A và B hiện nay có tổng là 36 tuổi. Biết tỉ số tuổi của A và B là 3:5. Tính tuổi của mỗi người. |
| Cách giải |
|
Qua bài toán trên, ta thấy rằng khi biết tổng và tỉ số tuổi, chúng ta có thể dễ dàng thiết lập phương trình để tìm ra tuổi của từng người. Việc luyện tập các bài toán này sẽ giúp học sinh nắm vững kỹ năng giải quyết vấn đề và tư duy logic trong toán học.
Dạng Bài Toán Tính Tuổi Với Sự Thay Đổi Tỉ Số Tuổi Theo Thời Gian
Dạng bài toán này yêu cầu bạn tính toán sự thay đổi tỉ số tuổi giữa các đối tượng theo thời gian. Thường trong bài toán, tỉ số tuổi sẽ thay đổi khi thời gian trôi qua, ví dụ như sau một số năm, tuổi của một người có thể tăng gấp đôi tuổi của người còn lại. Để giải quyết bài toán này, bạn cần áp dụng các phương pháp tính toán linh hoạt và xác định mối quan hệ giữa tuổi của các đối tượng qua các mốc thời gian khác nhau.
Để giải bài toán này, bạn có thể thực hiện các bước sau:
- Xác định tỉ số tuổi ban đầu của các đối tượng.
- Gọi tuổi của các đối tượng tại thời điểm hiện tại là các ẩn số, ví dụ tuổi của A là \(x\) và tuổi của B là \(y\).
- Thêm vào đó, biết được số năm sau đó và cách thức thay đổi tỉ số tuổi theo thời gian, bạn có thể thiết lập phương trình để tính toán sự thay đổi này.
- Giải phương trình để tìm ra độ tuổi mới của các đối tượng sau một khoảng thời gian.
Ví dụ chi tiết:
| Bài toán | Sau 5 năm, tuổi của A sẽ gấp đôi tuổi của B. Biết hiện nay tỉ số tuổi của A và B là 2:3. Tính tuổi hiện tại của A và B. |
| Cách giải |
|
Qua bài toán trên, ta thấy rằng khi biết tỉ số tuổi thay đổi theo thời gian, bạn cần chú ý đến sự biến động tỉ số qua các mốc thời gian nhất định để xác định đúng độ tuổi của từng đối tượng. Đây là dạng bài toán giúp học sinh phát triển khả năng giải quyết vấn đề và tư duy logic tốt hơn.

Dạng Bài Toán Với Số Thập Phân
Dạng bài toán với số thập phân trong toán lớp 5 giúp học sinh làm quen với việc sử dụng các phép toán cơ bản như cộng, trừ, nhân, chia với các số thập phân. Bài toán này không chỉ giúp các em nâng cao khả năng tính toán mà còn rèn luyện khả năng làm quen với các phép toán thực tế trong cuộc sống hằng ngày.
Để giải các bài toán với số thập phân, bạn cần chú ý đến cách sử dụng dấu phẩy và cách thực hiện phép tính sao cho chính xác. Các bài toán thường gặp trong dạng này là tính tổng, hiệu, tích hoặc thương của các số thập phân.
Ví dụ chi tiết:
| Bài toán | Chị Lan có 5.5 kg gạo, chị Mai có 3.7 kg gạo. Hỏi tổng số gạo của chị Lan và chị Mai là bao nhiêu kg? |
| Cách giải |
|
Trong bài toán này, bạn chỉ cần cộng hai số thập phân với nhau. Lưu ý khi cộng hoặc trừ số thập phân, bạn cần phải xếp các chữ số sau dấu thập phân thẳng hàng với nhau để đảm bảo phép tính chính xác.
Dạng bài toán này giúp các em học sinh nắm vững quy tắc làm việc với số thập phân, qua đó phát triển khả năng tư duy và khả năng ứng dụng toán học vào thực tiễn đời sống.
Dạng Bài Toán Khó Hơn: Giải Bài Toán Phức Tạp Về Tuổi Của Các Thành Viên Gia Đình
Dạng bài toán phức tạp về tuổi của các thành viên gia đình yêu cầu học sinh sử dụng nhiều phương pháp toán học khác nhau để giải quyết. Thông thường, bài toán sẽ đưa ra các mối quan hệ tuổi giữa các thành viên trong gia đình, có thể là qua tổng tuổi, tỉ số tuổi hoặc sự thay đổi tuổi theo thời gian. Những bài toán này không chỉ kiểm tra khả năng tính toán mà còn giúp học sinh rèn luyện kỹ năng phân tích và giải quyết vấn đề logic.
Để giải quyết các bài toán về tuổi của các thành viên trong gia đình, bạn cần thực hiện các bước sau:
- Xác định mối quan hệ tuổi giữa các thành viên trong gia đình. Thường thì bạn sẽ có mối quan hệ giữa tuổi của cha, mẹ, con, hoặc các anh chị em.
- Đặt ẩn số cho độ tuổi của các thành viên, sau đó thiết lập các phương trình dựa trên thông tin đã cho trong bài toán.
- Giải các phương trình để tìm ra độ tuổi của từng thành viên trong gia đình.
- Kiểm tra lại kết quả để đảm bảo tính chính xác của phép tính và phù hợp với đề bài.
Ví dụ chi tiết:
| Bài toán | Hiện nay, tổng tuổi của bố và con là 50 tuổi. Ba năm trước, tuổi của bố gấp ba lần tuổi của con. Hỏi tuổi hiện tại của bố và con? |
| Cách giải |
|
Bài toán này yêu cầu học sinh sử dụng phương pháp lập phương trình và giải hệ phương trình để tìm ra độ tuổi của các thành viên trong gia đình. Đây là dạng bài toán khá khó, nhưng với việc luyện tập, học sinh sẽ ngày càng cải thiện khả năng giải quyết các bài toán phức tạp và phát triển tư duy toán học.

Phương Pháp Và Kỹ Thuật Giải Toán Tính Tuổi Lớp 5
Giải toán tính tuổi trong chương trình Toán lớp 5 không chỉ giúp học sinh làm quen với các phép toán cơ bản mà còn phát triển kỹ năng suy luận logic. Các bài toán tính tuổi thường yêu cầu học sinh thiết lập phương trình từ các dữ liệu đã cho và sử dụng các phương pháp giải toán hợp lý. Dưới đây là một số phương pháp và kỹ thuật giải toán phổ biến giúp học sinh giải quyết các bài toán tính tuổi hiệu quả.
Để giải các bài toán tính tuổi, học sinh cần nắm vững các phương pháp cơ bản sau:
- Đặt ẩn số hợp lý: Khi giải bài toán về tuổi, bước đầu tiên là xác định các ẩn số cho tuổi của các đối tượng trong bài toán. Ví dụ, nếu bài toán có tuổi của A và B, ta có thể gọi tuổi của A là \(x\) và tuổi của B là \(y\).
- Thiết lập phương trình: Dựa vào các mối quan hệ giữa các đối tượng trong bài toán, bạn sẽ phải thiết lập phương trình. Các phương trình này có thể dựa trên tỉ số tuổi, tổng tuổi, hoặc sự thay đổi tuổi theo thời gian. Ví dụ, nếu tổng tuổi của A và B là 40, ta có phương trình \(x + y = 40\).
- Sử dụng phương pháp tỉ lệ: Trong một số bài toán, các đối tượng có thể có mối quan hệ về tỉ lệ tuổi (ví dụ, tuổi A gấp đôi tuổi B). Để giải các bài toán này, bạn sẽ dùng tỉ lệ để thiết lập phương trình và giải tìm giá trị của ẩn số. Ví dụ, nếu tuổi A gấp đôi tuổi B, ta có thể viết phương trình là \(x = 2y\).
- Phương pháp thay đổi theo thời gian: Trong nhiều bài toán, tuổi của các đối tượng thay đổi theo một khoảng thời gian nhất định (ví dụ, sau 5 năm nữa). Lúc này, bạn cần thêm các giá trị tương ứng vào các phương trình tuổi trong tương lai để giải bài toán. Ví dụ, nếu tuổi A sau 5 năm sẽ gấp ba lần tuổi B, ta có thể thiết lập phương trình mới và giải.
Ví dụ chi tiết:
| Bài toán | Hiện nay, tuổi của A gấp ba lần tuổi của B. Tổng tuổi của A và B là 48. Tính tuổi của A và B. |
| Cách giải |
|
Thông qua bài toán này, bạn có thể thấy rằng việc sử dụng phương trình và các kỹ thuật giải toán hợp lý giúp tìm ra giải pháp một cách nhanh chóng và chính xác. Học sinh có thể áp dụng các phương pháp này để giải quyết nhiều bài toán phức tạp hơn liên quan đến tuổi của các đối tượng trong cuộc sống.