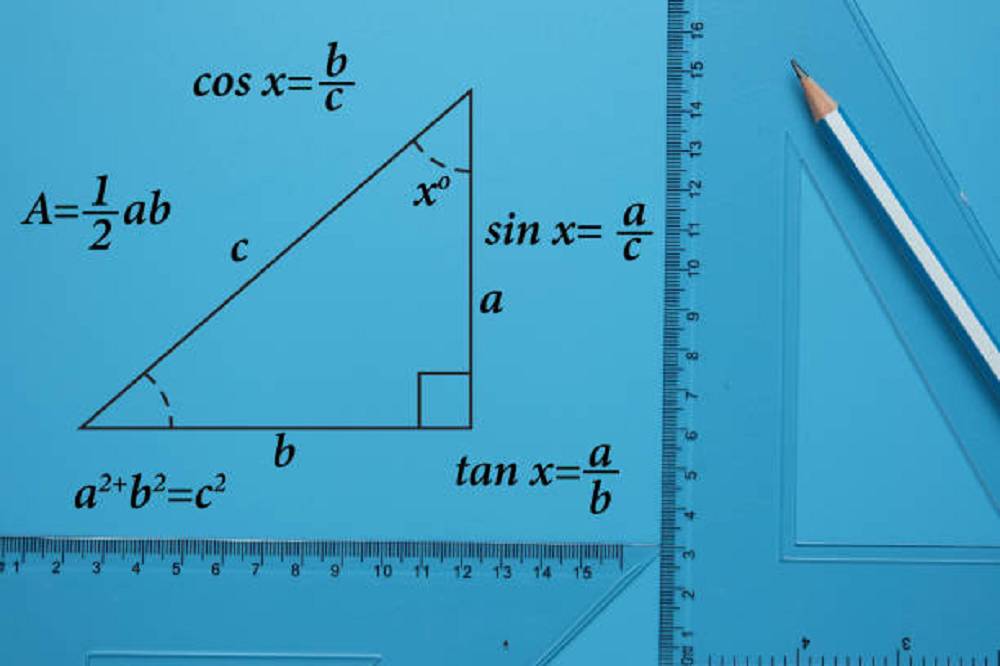Trí Tuệ 24h: Tìm hiểu công thức tính đạo hàm trong môn Toán

Trong môn Toán, việc hiểu và làm chủ công thức tính đạo hàm là một trong những kiến thức quan trọng. Để giúp các em học sinh nắm vững kiến thức này, chúng tôi sẽ cung cấp đến các bạn đọc về các công thức tính đạo hàm cơ bản và nâng cao nhất.

Định nghĩa cơ bản nhất về đạo hàm

Đạo hàm là tỉ số giữa số gia của hàm số và số gia của đối số tại điểm Xο. Giá trị của đạo hàm thể hiện chiều và độ lớn của biến thiên của hàm số.

Bạn đang xem: Trí Tuệ 24h: Tìm hiểu công thức tính đạo hàm trong môn Toán

Quy tắc cơ bản của đạo hàm

Dưới đây là bảng quy tắc cơ bản của đạo hàm:

Công thức tính đạo hàm của các hàm số cơ bản thường gặp

Dưới đây là bảng công thức tính đạo hàm của các hàm số cơ bản, thường gặp:

Công thức tính đạo hàm các hàm lượng giác

Công thức tính đạo hàm của các hàm lượng giác như sau:

• Đối với hàm số y = sin x: (sin x)’ = cos x
• Đối với hàm số y = cos x: (cos x)’ = – sin x
• Đối với hàm số y = tan x: (tan x)’ = sec²x
• Đối với hàm số y = cot x: (cot x)’ = -cosec²x

Công thức tính đạo hàm lượng giác ngược

Công thức tính đạo hàm lượng giác ngược như sau:

• Đối với hàm số y = arcsin(x): (arcsin(x))’ = 1 / √(1 – x²)
• Đối với hàm số y = arccos(x): (arccos(x))’ = – 1 / √(1 – x²)
• Đối với hàm số y = arctan(x): (arctan(x))’ = 1 / (1 + x²)
• Đối với hàm số y = arccot(x): (arccot(x))’ = – 1 / (1 + x²)
• Đối với hàm số y = arcsec(x): (arcsec(x))’ = 1 / IxI √( x² – 1)
• Đối với hàm số y = arccsc(x): (arccsc(x))’ = – 1 / IxI √( x² – 1)

Công thức đạo hàm cấp cao

Đạo hàm cấp cao là đạo hàm của đạo hàm cấp n-1. Dưới đây là bảng công thức đạo hàm cấp cao thường gặp:

Với những kiến thức về công thức tính đạo hàm mà chúng tôi đã chia sẻ ở trên, hi vọng các em đã nắm vững các kiến thức từ cơ bản đến nâng cao về công thức tính đạo hàm trong chương trình ôn thi đại học Toán lớp 12. Hãy tham khảo thêm tại Izumi.Edu.VN để được học thêm nhiều bài tập và kiến thức hữu ích khác.

Nguồn: https://izumi.edu.vn/
Danh mục: Công thức