Cách tính thể tích khối chóp và những ví dụ cụ thể cho các trường hợp

Chào các bạn! Bạn đã bao giờ tự hỏi làm thế nào để tính thể tích của khối chóp, khối lăng trụ, khối nón và khối trụ chưa? Đó là một câu hỏi khiến nhiều bạn đau đầu. Trong bài viết này, chúng ta sẽ tìm hiểu cách tính thể tích khối chóp và xem một số ví dụ cụ thể nhé.

Phương pháp tính thể tích khối chóp

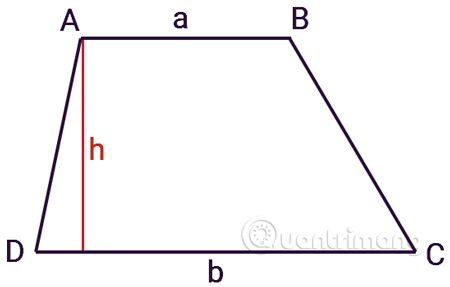
Công thức để tính thể tích khối chóp là: V = 1/3 B h, trong đó B là diện tích đáy và h là chiều cao của khối chóp. Để tính thể tích khối chóp, ta cần biết chiều cao và diện tích đáy của nó. Dưới đây là một số điểm cần chú ý khi xác định chiều cao trong các trường hợp sau:

Bạn đang xem: Cách tính thể tích khối chóp và những ví dụ cụ thể cho các trường hợp

• Nếu khối chóp là hình chóp đều, chiều cao của nó sẽ chạm tới tâm của đáy.
• Nếu khối chóp có mặt bên (SAiAk) vuông góc với mặt đáy, chiều cao của tam giác SAiAk sẽ là chiều cao của khối chóp.
• Nếu có hai mặt phẳng đi qua đỉnh và vuông góc với đáy, đường thẳng nối hai điểm giao của hai mặt phẳng đó sẽ là chiều cao của khối chóp.
• Nếu các cạnh bên của khối chóp bằng nhau, điểm chiếu của đỉnh sẽ là tâm của đường tròn ngoại tiếp đáy.
• Nếu các mặt bên tạo với đáy một góc bằng nhau, điểm chiếu của đỉnh sẽ là tâm của đường tròn nội tiếp đáy.

Những ví dụ cụ thể

Tính thể tích khối chóp có cạnh bên vuông góc với đáy

Dạng toán này cũng có thể được biểu diễn với hai mặt bên cùng vuông góc với đáy. Trong trường hợp này, chiều cao của khối chóp chính là đường thẳng nối hai mặt đó.

Ví dụ 1:
Cho khối chóp S.ABC có đáy là một tam giác đều với cạnh a. Cạnh bên SA vuông góc với mặt đáy. Hãy tính thể tích khối chóp S.ABC biết rằng cạnh bên SC tạo với mặt đáy góc 60º.

Lời giải:
Trong bài toán này, chúng ta đã biết đường cao là SA, nhưng chưa biết chiều dài của nó. Ta đã biết góc của một cạnh bên với đáy. Vì vậy, góc đó sẽ giúp ta tính chiều cao. Đáy là tam giác đều và đã biết chiều dài của cạnh. Do đó, ta có thể tính diện tích của đáy.

Tính thể tích khối chóp có mặt bên vuông góc với đáy

Trong trường hợp khối chóp có mặt bên (SAB) vuông góc với đáy, đường cao của hình chóp là SH, trong đó H là một điểm thuộc đường thẳng AB. Vấn đề thường gặp phải là xác định vị trí của điểm H. Thông thường, điểm H là một điểm đặc biệt nằm trên đường AB. Tuy nhiên, nếu chúng ta không thể xác định được điểm H, ta có thể sử dụng các công thức trong tam giác để tính độ dài SH.

Ví dụ 2:
Cho khối chóp S.ABCD có đáy là một hình vuông với cạnh a. Mặt bên (SAD) vuông góc với đáy. Biết rằng tam giác SAD vuông cân tại S. Hãy tính thể tích khối chóp A.ABCD.

Lời giải:
Gọi H là trung điểm của AD.
Vì tam giác SAD vuông cân tại S, ta có SH vuông góc với AD.
Vì mặt phẳng (SAD) vuông góc với đáy, ta có SH vuông góc với (ABCD).
Vì tam giác SAD vuông cân tại S, ta có:
Vậy thể tích khối chóp cần tính là:

Tính thể tích khối chóp đều

Khối chóp đều là khối chóp có đáy là một đa giác đều và hình chiếu của đỉnh lên mặt đáy trùng với tâm của đáy. Nếu đáy là một tam giác đều, tâm của nó chính là trọng tâm của tam giác. Đối với một tứ giác đều, nó chính là một hình vuông và tâm của nó là giao điểm của hai đường chéo. Thông thường, chúng ta chỉ quan tâm đến hai loại đáy này.

Ví dụ 3:
Hãy tính thể tích khối chóp tứ giác đều có tất cả các cạnh bằng a.

Lời giải:

Trên đây là cách tính thể tích khối chóp và một số ví dụ cụ thể cho các trường hợp. Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách tính toán này. Nếu bạn muốn tìm hiểu thêm, hãy ghé thăm Izumi.Edu.VN để biết thêm nhiều thông tin hữu ích nhé.

Nguồn: https://izumi.edu.vn/
Danh mục: Công thức