Học tập Toán: Cách tính diện tích lục giác đều

Hình lục giác, một hình đa giác có sáu cạnh, là một phần hình học phẳng thú vị. Tuy nhiên, làm thế nào để tính diện tích của một lục giác đều? Đồng thời, cách vẽ một lục giác đều như thế nào? Hãy cùng tìm hiểu trong bài viết dưới đây.

Có thể bạn quan tâm

Lục giác đều, một trong những kiến thức được học trong chương trình Toán lớp 6, 7, 8. Chúng ta hy vọng qua bài học này, bạn sẽ nắm vững khái niệm về hình lục giác, công thức tính diện tích cũng như cách vẽ một lục giác đều. Đừng quên tham khảo thêm tài liệu: bài tập hằng đẳng thức lớp 8, bài tập phân tích đa thức thành nhân tử.

Bạn đang xem: Học tập Toán: Cách tính diện tích lục giác đều

I. Công thức tính diện tích lục giác đều

Để tính diện tích của một hình lục giác thường, ta có thể chia nó thành 4 tam giác và tính tổng diện tích của các tam giác đó là diện tích của hình lục giác.

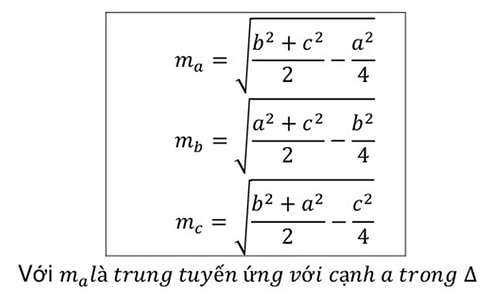
Công thức tính diện tích lục giác đều:

II. Cách tính diện tích lục giác đều

1. Tính diện tích lục giác đều khi biết độ dài một cạnh

Trường hợp đề bài cho sẵn độ dài một cạnh:

Đối với trường hợp này, bạn chỉ cần thay số đã cho vào công thức tính diện tích.

Trường hợp xác định độ dài qua chu vi (P):

Bạn có thể sử dụng công thức P = 6 x a để tìm cạnh của một hình lục giác đều bất kỳ. Sau khi xác định được chiều dài cạnh, bạn chỉ cần thay vào công thức tính diện tích.

Tính diện tích hình lục giác đều khi biết đường trung đoạn

Trung đoạn là đoạn thẳng vuông góc từ tâm của lục giác đều đến một cạnh bất kỳ.

2. Tính diện tích lục giác không đều khi biết các đỉnh

Bước 1: Xác định tọa độ các đỉnh của đa giác không đều.

Bạn hãy xác định tọa độ của tất cả các đỉnh lục giác bằng hệ trục tọa độ x, y. Khi biết tọa độ các đỉnh của một hình lục giác, bạn có thể dễ dàng tính được diện tích của nó.

Bước 2: Tạo bảng giá trị tọa độ.

Hãy lập một bảng liệt kê tọa độ x, y của mỗi đỉnh theo thứ tự ngược chiều kim đồng hồ và lặp lại giá trị đầu tiên ở cuối bảng.

Bước 3: Tính nhóm kết quả (1)

Lấy tọa độ x của đỉnh trước nhân với giá trị y của đỉnh tiếp theo rồi cộng các tích lại với nhau.

Bước 4: Tính nhóm kết quả hai (2)

Ngược với bước 3, tại bước này ta sẽ lấy tọa độ y của đỉnh trước nhân với tọa độ x của đỉnh tiếp theo rồi lấy tổng các tích.

Bước 5: Lấy tổng các tích của nhóm (1) trừ đi tổng các tích của nhóm (2) sau đó lấy trị tuyệt đối của kết quả.
Bước 6: Tính diện tích của lục giác không đều.

Thương của kết quả ở bước năm chia cho hai sẽ là diện tích của lục giác không đều.

III. Cách vẽ hình lục giác đều

3. Cách vẽ lục giác đều

Có nhiều cách vẽ hình lục giác đều mà bạn có thể tham khảo sau đây:

Cách 1: Vẽ đường tròn, trong hình tròn vẽ đường kính và lấy 2 điểm trên đường kính nằm trên đường tròn để vẽ 2 cung có bán kính bằng bán kính hình tròn ban đầu. Các điểm giao nhau của các hình tròn và hai đầu của đường kính sẽ tạo thành 6 đỉnh của lục giác đều.
Cách 2: Vẽ lục giác đều với độ dài cạnh cho trước. Lấy số đo độ dài cạnh làm bán kính để vẽ một đường tròn sau đó đặt liên tiếp các dây cung dài bằng bán kính đó lên đường tròn. Các điểm giao nhau của các dây cung liên tiếp sẽ tạo thành các đỉnh của lục giác đều.
Cách 3: Vẽ một tam giác đều sau đó vẽ cho nó một đường tròn ngoại tiếp từ một đỉnh của tam giác kéo dài qua tâm đường tròn cắt đường tròn tại một điểm khác. Từ điểm này, vẽ một tam giác đều có đường cao là đường kéo dài qua tâm hồi nãy.
Cách 4: Vẽ một đường tròn bất kỳ và đặt tâm ngay trên đường tròn. Quay các đường tròn đồng tâm với đường tròn ban đầu và cắt đường tròn ban đầu tại các điểm là đỉnh của lục giác cần tìm. Tâm của đường tròn sau là giao điểm của đường tròn ban đầu với các đường tròn trước đó.

IV. Bài tập tính diện tích lục giác đều

Bài 1: Cho lục giác lồi ABCDEF biết rằng mỗi đường chéo AD, BE, CF chia nó thành 2 phần có diện tích bằng nhau. Gọi M, N lần lượt là giao của EB với AC và FD, P và Q lần lượt là giao của AD với BF và CE. Chứng minh rằng:
a) PM song song với NQ.
b) AD, BE, CF đồng quy.
Bài 2: Chứng minh rằng nếu một ngũ giác có các góc bằng nhau và nội tiếp một đường tròn thì ngũ giác đó là ngũ giác đều.
Bài 3: Chứng minh rằng các cạnh đối diện AB và DE, BC và EF, CD và FA của lục giác ABCDEF song song. Chứng minh rằng diện tích tam giác ACE bằng diện tích tam giác BDF.
Bài 4: Cho lục giác ABCDEF có các cạnh đối diện song song.
a) Chứng minh rằng diện tích tam giác ACE lớn hơn hoặc bằng 1 nửa diện tích ABCDEF.
b) Chứng minh rằng nếu lục giác có các góc bằng nhau thì hiệu các cạnh đối diện bằng nhau.
Bài 5: Cho ngũ giác lồi ABCDE có tam giác ABC và CED đều. Gọi O là tâm tam giác ABC. M và N lần lượt là trung điểm của BD và AE. Chứng minh rằng tam giác OME và tam giác OND đồng dạng.