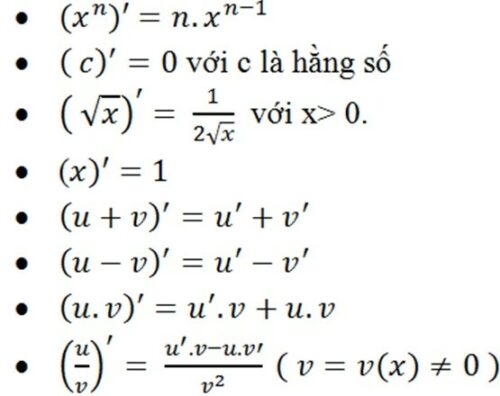Đạo hàm là một khái niệm quan trọng trong toán học, và nó có thể áp dụng vào rất nhiều lĩnh vực trong cuộc sống. Bài viết này sẽ giúp bạn hiểu rõ hơn về đạo hàm, từ khái niệm cơ bản đến các công thức nâng cao.
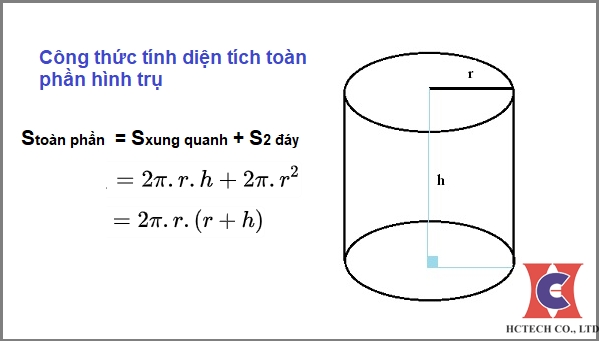
- Cách Tính Thể Tích Khối Trụ Tròn Xoay Và Bài Tập Hay
- Bảng Công Thức Lượng Giác Lớp 9, 10, 11: Tổng hợp đầy đủ nhất cho bạn
- Câu Tường Thuật (Reported Speech): Công Thức, Cách Dùng Và Bài Tập
- Cách tính thể tích khối chóp và những ví dụ cụ thể cho các trường hợp
- Tìm Hai Số Khi Biết Tổng Và Hiệu – Bài Toán Toán Học Thú Vị cho Học Sinh Lớp 4
1. Định nghĩa đạo hàm là gì?
Đạo hàm là một tỉ số giữa số gia của đối số và số gia của hàm số tại một điểm bất kỳ gọi là điểm x0. Chính giá trị của đạo hàm cho biết hướng biến thiên của hàm số. Đạo hàm có ứng dụng rất lớn trong vật lý, hình học và hình học không gian.
Bạn đang xem: Đạo hàm là gì? Khám phá khái niệm và các công thức từ cơ bản đến nâng cao
Ký hiệu đạo hàm: f’(x) hoặc y’(x).
.png)
2. Quy tắc tính đạo hàm dựa trên định nghĩa
Quy tắc tính đạo hàm dựa trên định nghĩa gồm các bước sau:
Bước 1: Giả sử là số gia của x tại x0. Lúc này ta tính số gia của hàm số f tại điểm x0.
Bước 2: Lập tỉ số giữa số gia của hàm số và số gia của đối số.
Bước 3: Tính giới hạn của tỉ số khi tiến tới 0.
Lưu ý: Nếu thay x0 bằng x, ta thu được công thức tính đạo hàm của hàm số y = f(x) với x thuộc đoạn (a, b).
3. Mối quan hệ giữa tính liên tục và sự tồn tại của đạo hàm
Một định lý quan trọng trong đạo hàm là nếu một hàm số có đạo hàm tại một điểm, thì nó sẽ liên tục tại điểm đó. Tuy nhiên, điều ngược lại chưa chắc đúng: một hàm số liên tục tại một điểm chưa chắc đã có đạo hàm tại điểm đó.
Ví dụ, hàm y = |x| liên tục tại x = 0, nhưng không có đạo hàm tại điểm đó.

4. Các công thức đạo hàm cần nhớ
Dưới đây là một số công thức đạo hàm cơ bản:
- (sin(x))’ = cos(x)
- (cos(x))’ = -sin(x)
Ngoài ra, còn có các bảng công thức đạo hàm đầy đủ, công thức đạo hàm của biến số, hàm số và phân thức hữu tỉ, bảng công thức đạo hàm và bảng nguyên hàm.
5. Các dạng bài liên quan tới đạo hàm
Có nhiều dạng bài tập khác nhau liên quan đến đạo hàm, bao gồm:
- Tính đạo hàm bằng định nghĩa.
- Chứng minh các đẳng thức liên quan tới đạo hàm.
- Viết phương trình tiếp tuyến khi được cho trước tiếp điểm.
- Viết phương trình tiếp tuyến khi biết hệ số góc.
- Phương trình và bất phương trình có đạo hàm.
- Dùng công thức đạo hàm nguyên hàm.
- Tính đạo hàm cấp cao.

6. Phương pháp giải bài tập đạo hàm hiệu quả
Để giải các bài tập đạo hàm hiệu quả, bạn cần làm theo các phương pháp sau:
- Nắm chắc công thức và định nghĩa của đạo hàm.
- Chăm chỉ giải lần lượt các bài tập từ cơ bản đến nâng cao.
- Luôn lưu ý về điều kiện của hàm số.
- Luôn note lại những lỗi sai và tự rút kinh nghiệm trong quá trình làm bài tập.
- Luôn kiên trì và chăm chỉ thực hành qua bài tập và đề thi.
Hy vọng rằng các thông tin trên đã giúp bạn hiểu rõ hơn về đạo hàm và các công thức liên quan. Để tìm hiểu thêm kiến thức về các môn khác, hãy truy cập Izumi.Edu.VN. Chúc bạn thành công trong việc ôn thi và học tập!
Nguồn: https://izumi.edu.vn/
Danh mục: Công thức