Công thức hình học không gian lớp 9: Những bí mật thú vị mà bạn chưa biết!

Các bạn học sinh lớp 9 hãy chuẩn bị tinh thần để khám phá những công thức hình học không gian thú vị trong bài viết này. Chúng ta sẽ cùng tìm hiểu về hình tam giác vuông, đường tròn và nhiều hình học khác. Hãy cùng khám phá!

Có thể bạn quan tâm

Công thức Toán lớp 9 Chương 1: Hình học

1. Hệ thức lượng trong tam giác vuông

Cho tam giác ABC có đường cao AH. Đặt BC = a, AC = b, AB = c, AH = h, CH = b’, BH = c’. BH, CH lần lượt là hình chiếu của AB và AC lên BC.

Bạn đang xem: Công thức hình học không gian lớp 9: Những bí mật thú vị mà bạn chưa biết!

Ta có các hệ thức sau:

b^2 = ab’ ; c^2 = ac’
h^2 = b’c’
ah = bc
a^2 = b^2 + c^2 (Định lý Py-ta-go)

2. Tỉ số lượng giác của góc nhọn

a) Định nghĩa
Công thức Toán lớp 9 Chương 1 Hình học chi tiết nhất

b) Tính chất

Cho hai góc α và β phụ nhau. Khi đó:
- sin(α) = cos(β)
- tan(α) = cot(β)
- cos(α) = sin(β)
- cot(α) = tan(β)
Cho góc nhọn α. Ta có:

d) Tỉ số lượng giác của các góc đặc biệt

3. Hệ thức về cạnh và góc trong tam giác vuông

Công thức Toán lớp 9 Chương 1 Hình học chi tiết nhất

b = asin(B) = acos(C)
b = ctan(B) = ccot(C)
c = asin(C) = acos(B)
c = btan(C) = bcot(B)

Công thức Toán lớp 9 Chương 2: Hình học

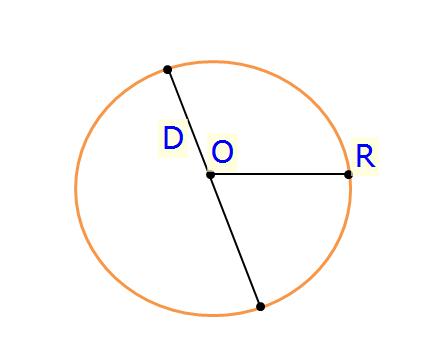
1. Sự xác định đường tròn

Một đường tròn được xác định khi biết tâm O và bán kính R của đường tròn đó (kí hiệu (O;R)), hoặc khi biết một đoạn thẳng là đường kính của đường tròn đó.
Có vô số đường tròn đi qua hai điểm. Tâm của chúng nằm trên đường trung trực của đoạn thẳng nối hai điểm đó.
Qua ba điểm không thẳng hàng, ta vẽ được một và chỉ một đường tròn.
Chú ý: Không vẽ được đường tròn nào đi qua ba điểm thẳng hàng.
Đường tròn đi qua ba đỉnh của tam giác gọi là đường tròn ngoại tiếp tam giác, tam giác gọi là tam giác nội tiếp đường tròn.

2. Tính chất đối xứng của đường tròn

Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó.
Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn.
Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.

3. Quan hệ giữa đường kính và dây của đường tròn

Trong các dây của một đường tròn, dây lớn nhất là đường kính.
Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.

4. Liên hệ giữa dây và khoảng cách từ tâm đến dây

Định lí 1: Trong một đường tròn:

Hai dây bằng nhau thì cách đều tâm.
Hai dây cách đều tâm thì bằng nhau.
AB = CD ⇔ OH = OK

Định lí 2: Trong hai dây của một đường tròn:

Dây nào lớn hơn thì dây đó gần tâm hơn.
Dây nào gần tâm hơn thì dây đó lớn hơn.
MN > CD ⇔ OI < OK

5. Vị trí tương đối của đường thẳng và đường tròn

Vị trí tương đối của đường thẳng và đường tròn:

Đường thẳng và đường tròn cắt nhau: 2, d < R
Đường thẳng và đường tròn tiếp xúc nhau: 1, d = R
Đường thẳng và đường tròn không giao nhau: 0, d > R

☞ Định lí: Nếu một đường thẳng a là tiếp tuyến của một đường tròn (O) thì nó vuông góc với bán kính đi qua tiếp điểm.
Đường thẳng a là tiếp tuyến của (O) ⇔ a ⊥ OI

6. Tính chất của hai tiếp tuyến cắt nhau

Định lí: Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:

Điểm đó cách đều hai tiếp điểm.
Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.

7. Vị trí tương đối của hai đường tròn

Cho (O ; R) và (O’; r) với R > r

VỊ TRÍ	HÌNH	SỐ ĐIỂM CHUNG	HỆ THỨC
Cắt nhau	2	A, B được gọi là 2 giao điểm	R – r < OO’ < R + r
Tiếp xúc ngoài	1	A gọi là tiếp điểm	OO’ = R + r
Tiếp xúc trong	1	A gọi là tiếp điểm	OO’ = R – r > 0
Không giao nhau ((O) và (O’) ở ngoài nhau)	0		OO’ > R + r
Không giao nhau ((O) đựng (O’) )	0		OO’ < R – r

☞ Định lí: Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng với nhau qua đường nối tâm, tức là đường nối tâm là đường trung trực của dây chung.
{A;B} = (O) ∩ (O’) ⇔ OO’ là trung trực của AB

Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm.
(O) tiếp xúc (O’) tại A ⇔ A ∈ OO’

Tiếp tuyến chung của hai đường tròn: Tiếp tuyến chung của hai đường tròn là đường thẳng tiếp xúc với cả hai đường tròn đó.

Công thức Toán lớp 9 Chương 2 Hình học chi tiết nhất

Mọi người cũng hỏi

Công thức hình học không gian lớp 9 bao gồm những nội dung gì?

Trả lời: Công thức hình học không gian lớp 9 thường bao gồm các khái niệm về hình vuông, hình chóp, hình cầu, hình trụ, tỉ lệ diện tích và thể tích. Các công thức này giúp tính diện tích bề mặt và thể tích của các hình học khác nhau.