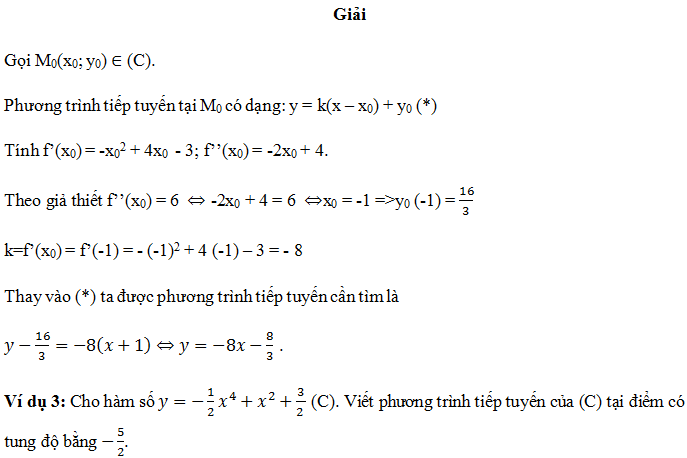Đạo Hàm Cấp Cao: Bí Mật Giấu Kín Trong Toán Học

Chào mừng các bạn đến với bài viết mới nhất của Izumi.Edu.VN! Hôm nay, chúng ta sẽ tiếp tục khám phá về đạo hàm cấp cao và các công thức đạo hàm thường gặp trong toán học. Hãy cùng tôi đi vào cuộc hành trình này và khám phá những bí mật thú vị nào!

Định nghĩa Đạo Hàm Cấp Cao

Giả sử chúng ta có một hàm số y = f(x) với đạo hàm f'(x). Đạo hàm của hàm số f'(x), nếu tồn tại, được gọi là đạo hàm cấp hai của hàm số f(x), ký hiệu là y” hoặc f”(x). Đạo hàm của hàm số f”(x), nếu tồn tại, được gọi là đạo hàm cấp ba của hàm số f(x), ký hiệu là y”’ hoặc f”'(x). Tương tự, đạo hàm của đạo hàm cấp (n-1) được gọi là đạo hàm cấp n của hàm số y = f(x), ký hiệu là y(n) hoặc f(n)(x).

Bạn đang xem: Đạo Hàm Cấp Cao: Bí Mật Giấu Kín Trong Toán Học

Đạo hàm cấp cao là một khái niệm quan trọng trong toán học, nó cho phép chúng ta tìm hiểu được một hàm số từ các khía cạnh khác nhau và giúp chúng ta giải quyết các bài toán phức tạp hơn.

Các Công Thức Đạo Hàm Thường Gặp

Đạo hàm của một hàm số không đổi (hằng số) luôn bằng 0. Ví dụ: 5′ = 0, 49′ = 0. Các quy tắc tính đạo hàm khác như sau:

• Đạo hàm của hàm số mũ (x^n) bằng n.x^(n-1).
• Đạo hàm của tổng hoặc hiệu của nhiều hàm số (u_1 ± u_2 ± … ± u_n) bằng tổng hoặc hiệu của các đạo hàm tương ứng (u_1′ ± u_2′ ± … ± u_n’).
• Đạo hàm của tích của hai hàm số (u.v) bằng đạo hàm của hàm số thứ nhất (u’) nhân với giá trị của hàm số thứ hai (v) cộng với hàm số thứ nhất (u) nhân với đạo hàm của hàm số thứ hai (v’).
• Đạo hàm của tích của một hằng số và một hàm số (c.u) bằng hằng số đó nhân với đạo hàm của hàm số (u).
• Đạo hàm của tích của ba hàm số (u.v.w) bằng đạo hàm của hàm số thứ nhất (u’) nhân với tích của hai hàm số còn lại (v.w), cộng với tích của hàm số thứ hai (u) nhân với đạo hàm của hàm số thứ ba (w’), cộng với tích của hai hàm số đầu nhân với đạo hàm của hàm số cuối cùng (v.w’).
• Đạo hàm của một phân số (frac{u}{v}) bằng hiệu giữa tích của đạo hàm của tử số (u’) nhân với mẫu số (v) trừ tích của tử số (u) nhân với đạo hàm của mẫu số (v’) chia cho bình phương của mẫu số (v^2).

Ngoài ra, chúng ta còn có công thức đạo hàm cho hàm số hợp, công thức đạo hàm cấp cao, và công thức Lepnit để giúp chúng ta giải quyết các bài toán phức tạp hơn. Đồng thời, trong bài viết này còn có một số bài tập mà chúng ta có thể tự luyện tập.

Kết Luận

Trên đây là những kiến thức cơ bản về đạo hàm cấp cao và các công thức đạo hàm thường gặp trong toán học. Qua bài viết này, hy vọng bạn đã hiểu thêm về cách tính đạo hàm cấp cao và cách áp dụng chúng vào giải quyết các bài toán. Đừng quên luyện tập thường xuyên để trở thành bậc thầy trong việc tính toán này nhé!

Để biết thêm thông tin về các khóa học và tư vấn học thuật, hãy truy cập Izumi.Edu.VN.

Hẹn gặp lại các bạn trong những bài viết tiếp theo của Izumi.Edu.VN!

Nguồn: https://izumi.edu.vn/
Danh mục: Công thức