Cách tính diện tích xung quanh hình nón đơn giản

Trong toán học, làm việc với hình nón là khá phổ biến. Hôm nay, mình sẽ chia sẻ với các bạn công thức tính diện tích xung quanh hình nón và những điều liên quan.

Hình nón là gì?

Trước khi tìm hiểu công thức tính diện tích xung quanh hình nón, chúng ta cần hiểu hình nón là gì.

Bạn đang xem: Cách tính diện tích xung quanh hình nón đơn giản

Hình nón là một hình học không gian ba chiều có bề mặt phẳng và bề mặt cong hướng lên trên. Đỉnh của hình nón được gọi là đỉnh, bề mặt phẳng được gọi là đáy.

Trên thực tế, chúng ta có thể thấy những vật dụng có hình dạng giống hình nón như nón lá, cây kem, mũ sinh nhật,…

Một số thuộc tính chính của hình nón bao gồm:

• Có một đỉnh hình tam giác.
• Một mặt tròn gọi là đáy hình nón.
• Không có bất kỳ cạnh nào.
• Chiều cao (h) – Khoảng cách từ tâm đường tròn đến đỉnh của hình nón. Hình tạo bởi đường cao và bán kính trong hình nón hình thành một tam giác vuông.

Công thức tính diện tích xung quanh hình nón

Diện tích xung quanh hình nón chỉ bao gồm diện tích mặt xung quanh, bao quanh hình nón, không tính diện tích đáy.

Công thức tính diện tích xung quanh hình nón là: Sxung quanh = π.r.l

Trong đó:

• Sxung quanh là diện tích xung quanh hình nón.
• r là bán kính đáy hình nón.
• l là độ dài đường sinh hình nón.

Như vậy, diện tích xung quanh hình nón bằng tích của số Pi (π) nhân với bán kính đáy hình nón nhân với độ dài đường sinh hình nón.

Hoặc có thể tính với công thức sau: “Diện tích xung quanh bằng một nửa tích của chu vi đường tròn đáy và độ dài đường sinh”. Bởi lẽ, π.r chính là nửa chu vi đường tròn.

Vậy là đã biết công thức tính diện tích xung quanh hình nón rồi. Hãy áp dụng vào bài toán thực tế để tránh sai sót đáng tiếc nhé.

Các công thức liên quan trong hình nón

Ngoài công thức tính diện tích xung quanh hình nón, còn có nhiều công thức khác trong hình nón như diện tích toàn phần và thể tích để giúp bạn giải quyết các bài toán liên quan.

Diện tích hình nón thường được chia thành hai loại: diện tích xung quanh và diện tích toàn phần. Chúng ta đã tìm hiểu về diện tích xung quanh ở phần trên, giờ ta tìm hiểu về diện tích toàn phần.

Công thức tính diện tích toàn phần hình nón

Diện tích toàn phần của hình nón bao gồm diện tích xung quanh và diện tích đáy tròn. Công thức tính diện tích toàn phần là tổng của diện tích xung quanh và diện tích đáy.

Công thức này có dạng: Stoàn phần = Sxung quanh + Sđáy = π.r.l + π.r^2

Thể tích hình nón

Thể tích hình nón là lượng không gian mà hình nón chiếm.

Công thức tính thể tích hình nón là diện tích đáy nhân với chiều cao.

Công thức này có dạng: Vhình nón = (1/3)π.r^2.h

Trong đó:

• V là thể tích hình nón.
• π là số Pi xấp xỉ 3,14.
• r là bán kính đáy hình nón.
• h là đường cao từ đỉnh xuống đáy hình nón.

Cách xác định đường sinh, đường cao và bán kính đáy của hình nón

• Đường cao là khoảng cách từ tâm đáy đến đỉnh của hình nón.
• Đường sinh là khoảng cách từ một điểm bất kỳ trên đường tròn đáy đến đỉnh của hình nón.

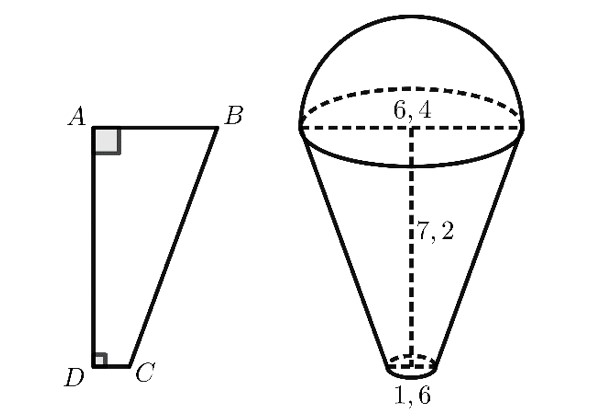
Do hình nón được tạo thành khi quay một tam giác vuông quanh trục góc vuông của nó một vòng, nên có thể coi đường cao và bán kính đáy là hai cạnh góc vuông của tam giác, còn đường sinh là cạnh huyền.

Với đường cao và bán kính đáy, ta có thể tính được đường sinh bằng công thức: l = √(r^2 + h^2)

Biết bán kính và đường sinh, ta tính đường cao theo công thức: h = √(l^2 – r^2)

Biết được đường cao và đường sinh, ta tính bán kính đáy theo công thức: r = √(l^2 – h^2)

Nhờ vào các cách xác định này, bạn có thể áp dụng công thức tính diện tích xung quanh hình nón vào các bài toán thực tế.

Một số ví dụ sử dụng công thức tính diện tích xung quanh hình nón

Ví dụ 1: Một hình nón có bán kính 3cm và chiều cao 5cm, tìm diện tích xung quanh của hình nón.

Đề bài cung cấp bán kính và chiều cao hình nón, tuy nhiên để tính diện tích xung quanh hình nón ta cần tìm đường sinh.

Đường sinh bằng cách tính tổng bình phương đường cao và bán kính. Áp dụng định lý Pythagore để tính giá trị đường sinh trong hình nón bất kỳ. Kết quả là l = 5.83 cm

Áp dụng công thức diện tích xung quanh hình nón đã đề cập ở trên ta có:
Sxung quanh = π.r.l = π.3.5,83 = 54,95 cm^2

Ví dụ 2: Cho biết diện tích toàn phần hình nón là 375 cm^2. Nếu đường sinh gấp bốn lần bán kính, thì đường kính cơ sở của hình nón là bao nhiêu? Sử dụng π = 3

Hướng dẫn giải như sau:
Theo đề bài: l = 4r và π = 3
Diện tích toàn phần hình nón là 375 cm^2 nên ta có: 3 × r × 4 r + 3 × r^2 = 375
<=> 12r^2 + 3r^2 = 375
<=> 15r^2 = 375
=> r = 5
Vậy bán kính mặt đáy hình nón là 5 => Đường kính mặt nón là 5.2 = 10 cm.

Hình nón cụt là gì?

Hình nón cụt là khi một mặt phẳng song song với đáy cắt một phần phía trên của hai hình nón, lúc này hình nón cụt không còn chóp đỉnh mà chỉ gồm hai mặt phẳng đáy.

• Bán kính của hình tròn đáy nhỏ hơn được gọi là bán kính nhỏ r1 và bán kính hình tròn đáy lớn hơn được gọi là bán kính r2.
• Khoảng cách được tính từ tâm hai đường kính đáy gọi là chiều cao của hình nón cụt.
• Đường sinh của hình nón cụt là l.
• π là hằng số Pi, xấp xỉ 3,14.

Công thức tính diện tích toàn phần của hình nón cụt:
Stp = π.(r1 + r2).l + π.r1^2 + π.r2^2

Trên đây là công thức tính diện tích xung quanh hình nón và các công thức liên quan trong hình nón. Tùy thuộc vào dữ liệu của bài toán mà bạn sẽ tùy biến để tìm ra kết quả chính xác.

Nguồn: https://izumi.edu.vn/
Danh mục: Công thức