Khoảng cách giữa 2 mặt phẳng trong không gian: Bí quyết giải quyết

Bạn đã bao giờ tự hỏi về khoảng cách giữa 2 mặt phẳng trong không gian? Bài viết này sẽ giúp bạn hiểu rõ hơn về vấn đề này.

Định nghĩa khoảng cách giữa 2 mặt phẳng

Trước khi đi vào chi tiết, chúng ta cần biết rằng trong không gian, có 3 vị trí tương đối giữa hai mặt phẳng. Đó là: mặt phẳng trùng nhau, mặt phẳng song song và mặt phẳng cắt nhau. Trong trường hợp mặt phẳng trùng nhau hoặc cắt nhau, khoảng cách giữa chúng được coi là 0 và không đòi hỏi tính toán. Do đó, chúng ta chỉ quan tâm đến khoảng cách giữa hai mặt phẳng song song.

Bạn đang xem: Khoảng cách giữa 2 mặt phẳng trong không gian: Bí quyết giải quyết

Định nghĩa:
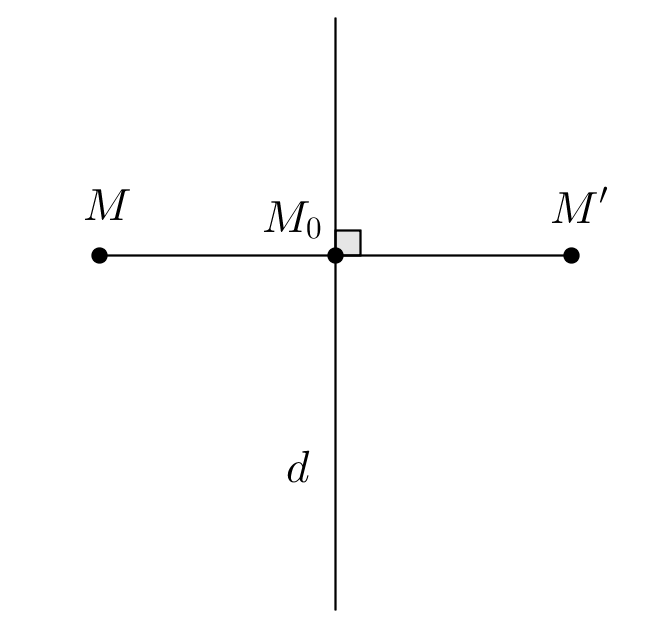
Khoảng cách từ một điểm M trên mặt phẳng (P) đến hình chiếu của M lên mặt phẳng (P) được ký hiệu là d(M,(P)).

Cho hai mặt phẳng (P) và (Q) song song với nhau, khoảng cách giữa mặt phẳng (P) và (Q) là khoảng cách từ một điểm M bất kỳ trên mặt phẳng (P) đến mặt phẳng (Q) hoặc ngược lại, được ký hiệu là d((P),(Q)).

Công thức tính khoảng cách giữa hai mặt phẳng

Cho hai mặt phẳng (P) và (Q) song song trong không gian. Phương trình của chúng có thể được chuyển về dạng:

(P): ax+by+cz+d=0 và (Q): ax+by+cz+d’=0 (a²+b²+c² > 0 và d ≠ d’)

Khi đó, giả sử điểm M(α;β;γ) thuộc mặt phẳng (P), ta có: aα + bβ + cγ = -d. Khoảng cách giữa (P) và (Q) chính là khoảng cách giữa điểm M và mặt phẳng (Q). Do đó, công thức tính khoảng cách giữa hai mặt phẳng song song là:

d((P),(Q)) = |(aα + bβ + cγ + d')| / √(a² + b² + c²)

Đơn giản và dễ hiểu phải không nào? :))

Ví dụ tính khoảng cách giữa 2 mặt phẳng

Hãy xem một ví dụ để minh họa công thức trên:

Ví dụ:
Tính khoảng cách giữa hai mặt phẳng (P): x+2y+2z+3=0 và (Q): 2x+4y+4z-11=0.

Lời giải:
Xem hình minh họa bên dưới để tìm câu trả lời.

Dễ dàng và nhanh chóng đúng không? Chúc bạn thành công!

Bạn cũng có thể tìm hiểu thêm về các chủ đề khác như:

• Phương trình mặt cầu và các dạng bài tập
• Phương pháp tọa độ trong không gian
• Khoảng cách từ điểm đến mặt phẳng trong không gian
• Khoảng cách giữa đường thẳng và mặt phẳng hình Oxyz
• Công thức tính khoảng cách giữa 2 điểm
• Khoảng cách giữa 2 đường thẳng trong oxyz
• Vị trí tương đối của 2 đường thẳng trong không gian
• Công thức tính góc giữa 2 mặt phẳng
• Khoảng cách từ điểm đến đường thẳng trong oxyz
• Phương pháp tọa độ Oxyz

Hy vọng những kiến thức này sẽ giúp ích cho bạn.

Nguồn: https://izumi.edu.vn/
Danh mục: Công thức