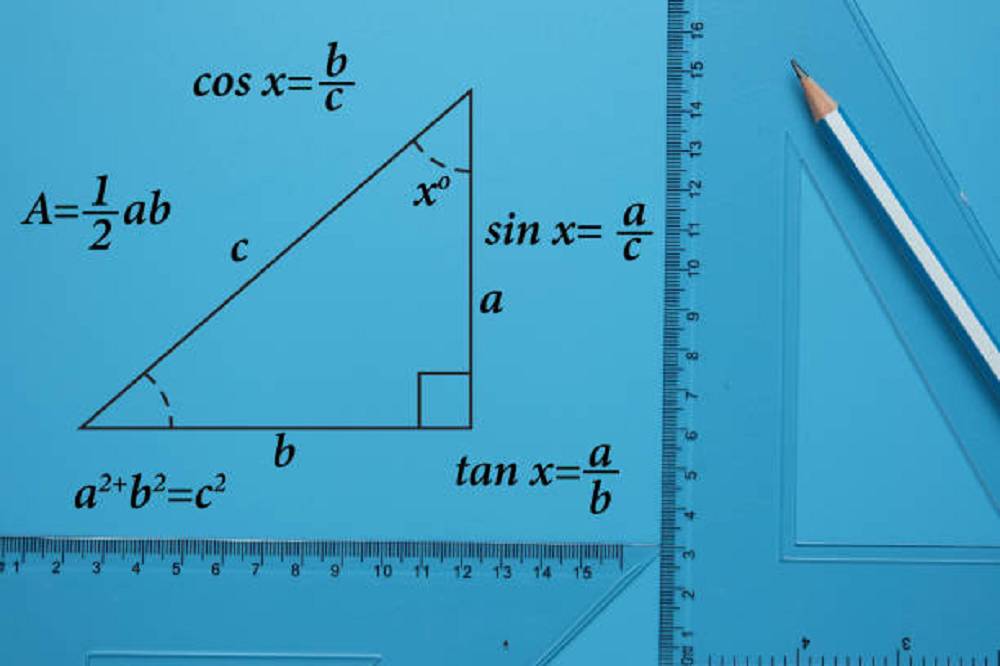Trong môn Toán, công thức lượng giác là một trong những nội dung khó nhất. Việc nhớ hàng chục công thức sin cos tan dài dằng dặc chắc chắn không dễ. Dưới đây là tổng hợp 50 công thức lượng giác cơ bản và nâng cao giúp bạn ôn tập nhanh cho bài thi giữa kì sắp tới.
1. Tổng Hợp Các Công Thức Lượng Giác Cơ Bản Nhất
Bài toán lượng giác không khó nhưng cũng không dễ dàng chút nào. Để giải quyết một bài toán, cần phải kết hợp nhiều kiến thức. Tuy nhiên, cốt lõi luôn nằm ở các công thức lượng giác cơ bản nhất. Vì vậy, hãy dành thời gian nắm chắc các công thức này.
Bạn đang xem: 50 Công Thức Lượng Giác Cơ Bản – “Siêu Tốc Độ” Cho Bài Thi Giữa Kì
a) Hai Cung Đối Nhau (α và – α)
- cos α = cos (- α)
- sin α = – sin (- α)
- tan α = – tan (- α)
- cot α = – cot (- α)
b) Hai Cung Bù Nhau (α và π – α)
- sin (π – α) = sin α
- cos (π – α) = – cos α
- tan (π – α) = – tan α
- cot (π – α) = – cot α
Tóm lại, đối với các cung liên quan đặc biệt, bạn có thể nhớ theo cách ngắn gọn: “cos đối, sin bù, phụ chéo; khác pi tan (cot)”. Nghĩa là cos các góc đối thì bằng nhau, sin các góc bù thì bằng nhau, sin cos các góc phụ nhau thì đối nhau, còn tan và cot các góc khác nhau pi/2 sẽ bằng nhau.
.png)
2. Một Số Bài Thơ Vui Giúp Nhớ Nhanh Các Công Thức Lượng Giác
Ngoài việc học thuộc bằng thơ, cách học này cũng được nhiều học sinh áp dụng. Phương pháp này giúp bạn dễ dàng thuộc các công thức lượng giác một cách nhanh chóng và thành thạo.
Thơ Vui Công Thức Lượng Giác Biến Tổng Thành Tích
- Cos + Cos = 2 cos cos
- Cos – Cos = – 2 sin sin
- Sin + Sin = 2 sin cos
- Sin – Sin = 2 sin sin
- Tan ta cộng với tan mình bằng sin hai đứa trên cos mình cos ta
Thơ Vui Công Thức Lượng Giác Biến Đổi Tích Thành Tổng
- Cos cos nửa cos-cộng, cộng cos-trừ
- Sin sin nửa cos-trừ trừ cos-cộng
- Sin cos nửa sin-cộng cộng sin-trừ
Thơ Vui Công Thức Lượng Giác Trong Tam Giác Vuông Bài 1
- Sao đi học (sin = đối/ huyền)
- Cứ khóc hoài (cos = kề/ huyền)
- Thôi đừng khóc (tan = đối/ kề)
- Có kẹo đây (cot = kề/ đối)
Thơ Vui Công Thức Lượng Giác Trong Tam Giác Vuông Bài 2
- Hoặc một cách nhớ công thức sin cos trong tam giác vuông khác nhé. Ngoài cách nhớ lâu các công thức lượng giác theo phương pháp truyền thống, các bài thơ chắc chắn sẽ giúp bạn thấy việc học công thức lượng giác trở nên dễ dàng hơn rất nhiều.
- Tìm sin lấy đối chia huyền
- Cosin lấy cạnh kề, huyền chia nhau.
- Còn tang ta tính như sau:
- Đối trên, kề dưới chia nhau ra liền.
- Cotang cũng dễ ăn tiền,
- Kề trên, đối dưới chia liền là ra
Thơ Vui Công Thức Lượng Giác Nhân Đôi
- Sin gấp đôi = 2 sin cos
- Cos gấp đôi = bình cos trừ bình sin
- Tang gấp đôi
- Tang đôi ta lấy đôi tang (2 tang) Chia 1 trừ lại bình tang, ra liền.
Cách Nhớ Công Thức Đặc Biệt: tan(a+b)=(tan+tanb)/1-tana.tanb
- tan một tổng 2 tầng cao rộng trên thượng tầng tan + tan tan dưới hạ tầng số 1 ngang tàng dám trừ một tích tan tan oai hùng
Thơ Vui Công Thức Lượng Giác Nhân Ba
- Nhân ba một góc bất kỳ,
- sin thì ba bốn, cos thì bốn ba,
- dấu trừ đặt giữa 2 ta, lập phương chỗ bốn thế là ok.
- Tang đôi ta lấy đôi tang (2 tang)
- Chia 1 trừ lại bình tang, ra liền.
3. Cách Học Công Thức Lượng Giác Trong Các Bài Toán Biến Đổi
Nếu chỉ học thuộc vẹt các công thức lượng giác, bạn sẽ thấy rất chán nản. Thay vào đó, hãy áp dụng công thức ngay sau khi học vào bài tập biến đổi. Sau khi làm các bài tập biến đổi lượng giác, bạn sẽ học thuộc được các công thức một cách dễ dàng. Đây chính là cách học công thức lượng giác cực kì hiệu quả. Trong quá trình biến đổi, cần chú ý các phương pháp sau:
Hạ Bậc
- Phương pháp hạ bậc khi thực hiện cần kết hợp với các hằng đẳng thức, chủ yếu là bậc hai, bậc ba và bậc bốn. Nên nắm chắc các hằng đẳng thức trước để có thể hạ bậc của các hàm lượng giác. Khi gặp các bậc cao trong một bài toán, cách áp dụng công thức lượng giác phù hợp là chuyển đổi xuống bậc thấp để tính toán dễ hơn.
Biến Tích Thành Tổng và Tổng Thành Tích
- Sử dụng phương pháp biến tích thành tổng, tổng thành tích để xuất hiện các nhóm giống nhau và rút gọn chúng. Dấu hiệu quan trọng để thực hiện phép biến đổi này là tổng hoặc hiệu của hai cung có liên quan đến cung thứ 3 trong bài toán.
Chú Ý Đến Các Góc Đặc Biệt
Các cung đặc biệt là công thức lượng giác căn bản đầu tiên mà bạn cần nhớ. Khi áp dụng cách học công thức lượng giác vào quá trình biến đổi lượng giác, cần chú ý đến các biểu thức, cố gắng đưa chúng về những góc đặc biệt để triệt tiêu các phần tử dư thừa nhanh nhất.
Tổng hợp trên là toàn bộ cách học công thức lượng giác nhanh nhất cùng các kiến thức cơ bản trong chuyên đề lượng giác. Bao gồm công thức lượng giác của các góc đặc biệt (đối, bù, phụ), công thức cộng, trừ, nhân đôi, và đặc biệt là hệ thức lượng trong tam giác. Chúc bạn học tốt!
Nguồn: https://izumi.edu.vn/
Danh mục: Công thức