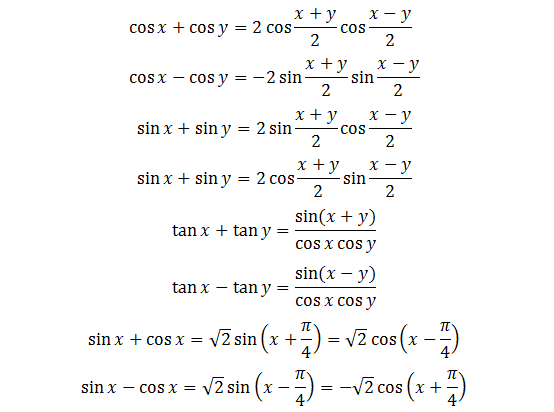Công thức delta là một phần kiến thức quan trọng trong chương trình môn Toán lớp 9. Để nắm vững kiến thức và chuẩn bị tốt cho các kỳ thi quan trọng, hãy cùng tìm hiểu về công thức tính Delta trong bài viết này.
1. Định nghĩa về Delta trong toán học
Delta là một chữ cái trong bảng chữ cái Hy Lạp, được kí hiệu là Δ (đối với chữ hoa) và δ (đối với chữ thường). Trong toán học lớp 9, kí hiệu Δ được sử dụng để chỉ một biệt thức trong phương trình bậc hai. Giá trị của delta giúp xác định số nghiệm của phương trình bậc hai và cũng được sử dụng để kí hiệu cho đường thẳng trong một số trường hợp.
Bạn đang xem: Tìm hiểu về công thức Delta và cách áp dụng trong giải toán toán học
.png)
2. Định nghĩa phương trình bậc hai một ẩn
Phương trình bậc hai một ẩn có dạng:
ax^2 + bx + c = 0
3. Công thức nghiệm của phương trình bậc hai một ẩn
Để giải phương trình bậc hai một ẩn, chúng ta có thể sử dụng một trong hai công thức sau:
x1 = (-b + √Δ) / (2a) x2 = (-b - √Δ) / (2a)

4. Công thức Delta trong phương trình bậc hai một ẩn
Trong phương trình bậc hai một ẩn, công thức Delta có dạng:
Δ = b^2 - 4ac
5. Công thức tính Delta phẩy
Công thức tính Delta phẩy có dạng:
Δ' = -b^2 + 4ac

6. Các dạng bài tập sử dụng cách tính delta bằng máy tính và delta phẩy
Công thức delta có thể được áp dụng để giải phương trình bậc hai một ẩn và cũng giúp bạn lý luận về nghiệm của phương trình. Bên cạnh đó, bạn cũng có thể sử dụng công thức tính delta trên máy tính để có kết quả chính xác và nhanh chóng. Dưới đây là một số ví dụ bài tập áp dụng công thức delta:
6.1. Ví dụ 1, 2, 3, 4
- Bài 1: Giả sử phương trình: x² + ax + b + 1 = 0 có hai nghiệm, hãy chứng minh a² + b² là một hợp số.
- Bài 2: Chứng minh phương trình sau có nghiệm với mọi a, b: (a+1) x² – 2 (a + b)x + (b- 1) = 0.
- Bài 3: Cho phương trình x² – 2(m+1)x + m² + m +1 = 0. Tìm các giá trị của m để phương trình có nghiệm. Hãy tính nghiệm x1, x2 theo m.
- Bài 4: Cho phương trình (2m – 1)x² – 2(m + 4 )x +5m + 2 = 0 (m #½). Tìm giá trị m để phương trình có nghiệm. Sau đó tính tổng S và tích P của hai nghiệm.
6.2. Ví dụ 5, 6, 7
- Bài 5: Cho f(x) = x² – 2(m +2)x + 6m +1. Chứng minh phương trình luôn có nghiệm với mọi m. Tìm điều kiện của m để phương trình f(x) = 0 có hai nghiệm lớn hơn 2.
- Bài 6: Cho phương trình: 2x² + (2m – 1)x +m – 1 =0. Chứng minh phương trình có nghiệm với mọi m. Xác định m để phương trình có hai nghiệm x1, x2 thỏa mãn -1 < x1 < x2 < 1.
- Bài 7: Phương trình x² – 6x + m = 0. Tính giá trị của m, trong đó 2 nghiệm thỏa mãn điều kiện x1 – x2 = 4.
6.3. Ví dụ 8, 9
- Bài 8: Cho phương trình (x²)² – 13 x² + m = 0. Tìm các giá trị của m để phương trình thỏa mãn một trong các điều kiện như: có bốn nghiệm phân biệt, có ba nghiệm phân biệt, có hai nghiệm phân biệt, có một nghiệm, vô nghiệm.
- Bài 9: Cho phương trình bậc hai f(x) = ax² + bx +c với điều kiện Ι f(x)Ι =< 1. Tìm giá trị nhỏ nhất của biểu thức A= 4a² + 3b².
Qua những ví dụ trên, bạn sẽ có cơ hội thực hành và nâng cao kiến thức toán học của mình. Hãy áp dụng cách tính delta bằng máy tính để tiết kiệm thời gian và đạt được độ chính xác cao. Bài viết này nhằm giúp bạn hiểu rõ hơn về công thức delta và áp dụng chúng trong giải toán bậc hai. Hãy tiếp tục theo dõi những bài viết tiếp theo để có thông tin hữu ích khác.
Nguồn: https://izumi.edu.vn/
Danh mục: Công thức