Bạn đã từng nghe về đường phân giác trong tam giác chưa? Hôm nay, mình sẽ giới thiệu cho các bạn định nghĩa, tính chất và công thức tính độ dài của đường phân giác trong tam giác. Đồng thời, mình cũng sẽ cung cấp lời giải chi tiết cho bài tập áp dụng kiến thức về đường phân giác. Hãy cùng khám phá ngay thôi!
- Tổng hợp Lý thuyết Vật Lí lớp 12 Học kì 2 đầy đủ, chi tiết – Vật Lí lớp 12
- Cách tính lãi suất gửi tiết kiệm ngân hàng dễ hiểu nhất
- Bí kíp đọc và hiểu công thức đạo hàm logarit, căn bậc 3 và lượng giác
- Etyl Propionat – Một loại Este thơm ngon giống mùi quả dứa
- Lý thuyết và các dạng bài tập về rơi tự do – Vật lý 10
I. Định nghĩa đường phân giác trong tam giác
Đường phân giác trong tam giác là đường thẳng chia góc đó thành hai góc có độ lớn bằng nhau. Mỗi tam giác có ba đường phân giác và chúng đồng quy với nhau tại một điểm gọi là tâm đường tròn nội tiếp tam giác.
Bạn đang xem: Đường phân giác – Khám phá định nghĩa, tính chất và công thức tính độ dài
Ví dụ: Trong tam giác ABC, ta có 3 đường phân giác AH, CP, BK và chúng giao nhau tại điểm O.
.png)
II. Tính chất đường phân giác trong tam giác
Đường phân giác trong tam giác có tính chất sau:
- Ba đường phân giác trong tam giác đồng quy với nhau tại một điểm, điểm đó được gọi là tâm đường tròn nội tiếp tam giác.
- Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề của đoạn thẳng đó. Tính chất này cũng đúng đối với đường phân giác góc ngoài tam giác.
Ví dụ: Trong tam giác ABC, chúng ta có 3 đường phân giác AH, CP, BK.
- 3 đường phân giác đồng quy tại điểm O, O là tâm đường tròn nội tiếp tam giác ABC.
- (HB/BK = AB/BC), (PA/PC = AC/BC), (KA/KC = AB/BC)
Lưu ý: Không chỉ áp dụng trong tam giác thường, đường phân giác cũng tồn tại và có tính chất như vậy trong các tam giác vuông, tam giác cân và tam giác đều.
Đường phân giác trong tam giác cân và tam giác đều
- Đường phân giác trong tam giác cân hạ từ đỉnh cân xuống cạnh đáy và là đường trung tuyến, đường trung trực, đường cao của tam giác.
- Đường phân giác trong tam giác đều hạ từ 3 đỉnh và cũng là đường trung tuyến, đường trung trực, đường cao của tam giác.
III. Công thức độ dài của đường phân giác
Công thức chung:
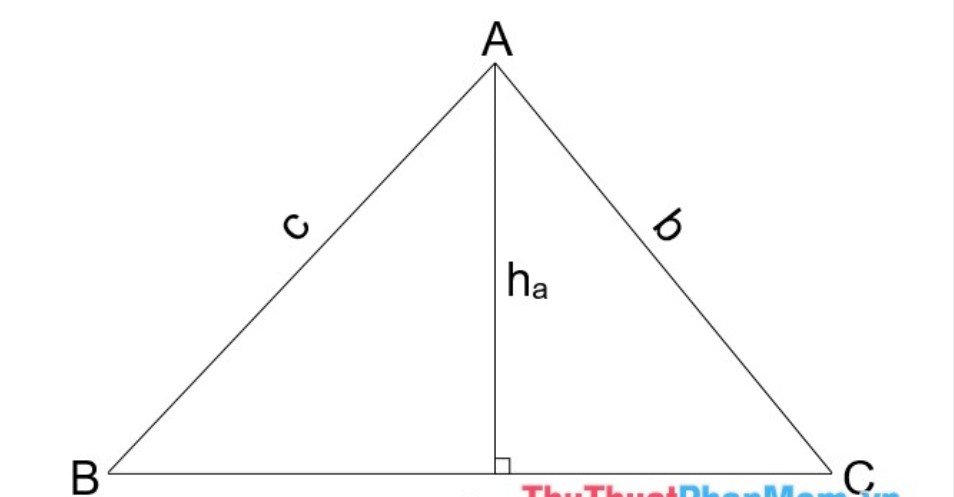
Công thức tính độ dài đường phân giác của một tam giác dựa vào độ dài hai cạnh bên và số đo góc chứa đường phân giác như sau:
m = (2bc*cosα)/(b+c)
Trong đó:
- m: Độ dài đường phân giác của tam giác.
- b, c: Độ dài cạnh của tam giác.
- α: Số đo góc chứa đường phân giác.
Đường phân giác trong tam giác đều
Đường phân giác tam giác đều có độ dài bằng nhau. Áp dụng định lý Heron, ta có công thức tính độ dài đường phân giác trong tam giác đều như sau:
m = (a√3)/2
Trong đó:
- m: Độ dài đường phân giác của tam giác đều.
- a: Cạnh của tam giác đều.

IV. Bài tập minh họa về công thức độ dài của đường phân giác
Ví dụ: Cho hình tam giác ABC có đường cao AD (D thuộc BC), biết AB = 10m, AC = 12m, ∠BAC = 60°. Hãy tính độ dài đường phân giác trong AD.
Lời giải tham khảo:
Áp dụng công thức tính độ dài đường phân giác, ta có:
AD = (2 10 12 * cos 60°)/(10 + 12) = 60/11
Vậy độ dài đường phân giác trong AD là 60/11.
Đó là những điều cơ bản về đường phân giác trong tam giác mà mình muốn chia sẻ với các bạn. Hy vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về định nghĩa, tính chất và công thức tính độ dài của đường phân giác. Nếu bạn cần thêm thông tin, hãy ghé thăm Izumi.Edu.VN để tìm kiếm nhiều kiến thức hơn nhé!
Đường phân giác – Những bí mật không thể bỏ qua!
Nguồn: https://izumi.edu.vn/
Danh mục: Công thức